题目内容
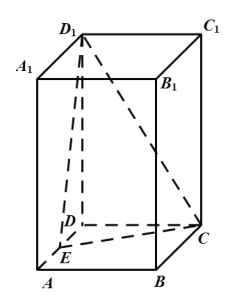
【题目】如图:多面体![]() 中,四边形
中,四边形![]() 为矩形,二面角
为矩形,二面角![]() 为60°,
为60°,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
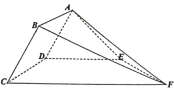
(1)求证:![]() 平面
平面![]() ;
;
(2)![]() 线段
线段![]() 上一点,若锐二面角
上一点,若锐二面角![]() 的正弦值为
的正弦值为![]() ,求
,求![]() .
.
【答案】(1)证明见解析
(2)![]()
【解析】
(1)通过证明面![]() 面
面![]() ,从而得到
,从而得到![]() 面
面![]() .
.
(2)由题意知:![]() ,
,![]() ,则
,则![]() 即为二面角
即为二面角![]() 的平面角,
的平面角,
因为![]() ,
,![]() ,
,![]() 两两垂直,故以
两两垂直,故以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() ,
,![]() 轴建立如图所示直角坐标系,设
轴建立如图所示直角坐标系,设![]() ,利用空间向量法求二面角从而得到方程解得.
,利用空间向量法求二面角从而得到方程解得.
(1)证明:四边形![]() 为矩形,
为矩形,
![]() ,
,![]() 面
面![]() ,
,![]() 面
面![]() ,
,
![]() 平面
平面![]() ,
,
![]() ,
,![]() 面
面![]() ,
, ![]() 面
面![]() ,
,
![]() 面
面![]() ,
,
![]() ,
,![]() 面
面![]() ,
,
![]() 面
面![]() 面
面![]() ,
,
![]() 面
面![]() ,
,
![]() 面
面![]()
(2)解:由题意知:![]() ,
,![]() ,
,
![]() 即为二面角
即为二面角![]() 的平面角,
的平面角,
![]() ,
,![]() 面
面![]() ,在平面
,在平面![]() 上过
上过![]() 作
作![]() ,
,![]()
![]() ,
,![]() ,
,![]() 两两垂直,故以
两两垂直,故以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() ,
,![]() 轴建立如图所示直角坐标系
轴建立如图所示直角坐标系
设![]()
![]() ,
,![]() ,
,![]()
![]() 面
面![]() ,面
,面![]() 法向量
法向量![]()
设面![]() 法向量为
法向量为![]() ,
,
![]() ,
,![]()
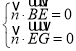 得
得 令
令![]() 得,
得,![]()
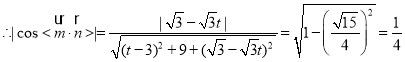
![]() ,解之可得:
,解之可得:![]() ,
,![]()
![]() (舍)
(舍) ![]() ,
,

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
【题目】![]() 是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物),为了探究车流量与
是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物),为了探究车流量与![]() 的浓度是否相关,现采集到某城市周一至周五某时间段车流量与
的浓度是否相关,现采集到某城市周一至周五某时间段车流量与![]() 浓度的数据如下表:
浓度的数据如下表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量 | 50 | 51 | 54 | 57 | 58 |
| 39 | 40 | 42 | 44 | 45 |
(1)根据上表数据,求出这五组数据组成的散点图的样本中心坐标;
(2)用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若周六同一时间段车流量是100万辆,试根据(2)求出的线性回归方程预测,此时![]() 的浓度是多少?
的浓度是多少?
(参考公式: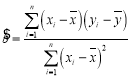 ,
,![]() )
)