题目内容
已知函数f(x)=sin
cos
+
sin(x+
).
(1)写出f(x)的最小正周期以及单调区间;
(2)若函数h(x)=cos(x+
),求函数y=log2(f(x)•h(x))的最大值,以及使其取得最大值的x的集合.
| x |
| 2 |
| x |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
(1)写出f(x)的最小正周期以及单调区间;
(2)若函数h(x)=cos(x+
| 5π |
| 4 |
(1)f(x)=
sinx+
cosx=
sin(x+
),
∵ω=1,∴T=2π;
令-
+2kπ≤x+
≤
+2kπ,k∈Z,解得:-
+2kπ≤x≤
+2kπ,k∈Z,
令
+2kπ≤x+
≤
+2kπ,k∈Z,解得:
+2kπ≤x+
≤
+2kπ,k∈Z,
则f(x)的单调递增区间为[-
+2kπ,
+2kπ],k∈Z;单调递减区间为[
+2kπ,
+2kπ],k∈Z;
(2)∵f(x)•h(x)=
sin(x+
)cos(x+
)
=-
sin(x+
)cos(x+
)=-
sin(2x+
)=-
cos2x,
∴y=log2(f(x)•h(x))=log2(-
cos2x),
∴ymax=log2
=-
,
当cos2x=-1,即x={x|x=
+kπ,k∈Z}时,y取得最大值.
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 4 |
∵ω=1,∴T=2π;
令-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 4 |
| π |
| 4 |
令
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
则f(x)的单调递增区间为[-
| 3π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
(2)∵f(x)•h(x)=
| ||
| 2 |
| π |
| 4 |
| 5π |
| 4 |
=-
| ||
| 2 |
| π |
| 4 |
| π |
| 4 |
| ||
| 4 |
| π |
| 2 |
| ||
| 4 |
∴y=log2(f(x)•h(x))=log2(-
| ||
| 4 |
∴ymax=log2
| ||
| 4 |
| 3 |
| 2 |
当cos2x=-1,即x={x|x=
| π |
| 2 |

练习册系列答案
相关题目
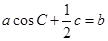 .
.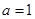 ,求△ABC的周长L的取值范围.
,求△ABC的周长L的取值范围.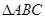 中,角
中,角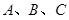 所对的边为
所对的边为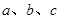 ,且满足
,且满足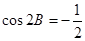 ,
,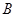 的值;(2)若
的值;(2)若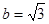 且
且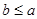 ,求
,求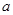 的取值范围.
的取值范围.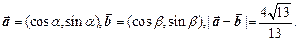
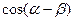 的值; (2)若
的值; (2)若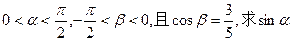 的值。
的值。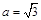 ,B=
,B=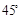 , ,求角A.经推断破损处的条件为三角形一边的长度,且答案提示A=
, ,求角A.经推断破损处的条件为三角形一边的长度,且答案提示A=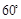 ,请将条件补完整.
,请将条件补完整.