题目内容
已知函数f(x)=2cos2
+sinx-1
(1)求函数f(x)的最小正周期和值域;
(2)若x∈(
,
),且f(x)=
,求sinx的值.
| x |
| 2 |
(1)求函数f(x)的最小正周期和值域;
(2)若x∈(
| π |
| 2 |
| 3π |
| 4 |
| 1 |
| 5 |
(1)∵f(x)=cosx+sinx=
cos(x-
),
∴函数f(x)的周期为2π,
又∵-1≤cos(x-
)≤1,
则函数f(x)的值域为[-
,
];
(2)∵f(x)=
cos(x-
)=
,
∴cos(x-
)=
,
∵x∈(
,
),∴x-
∈(
,
),
∴sin(x-
)=
=
,
则sinx=sin[(x-
)+
]=sin(x-
)cos+cos(x-
)sin
=
×
+
×
=
.
| 2 |
| π |
| 4 |
∴函数f(x)的周期为2π,
又∵-1≤cos(x-
| π |
| 4 |
则函数f(x)的值域为[-
| 2 |
| 2 |
(2)∵f(x)=
| 2 |
| π |
| 4 |
| 1 |
| 5 |
∴cos(x-
| π |
| 4 |
| ||
| 10 |
∵x∈(
| π |
| 2 |
| 3π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
∴sin(x-
| π |
| 4 |
1-cos2(x-
|
7
| ||
| 10 |
则sinx=sin[(x-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
=
7
| ||
| 10 |
| ||
| 2 |
| ||
| 10 |
| ||
| 2 |
| 4 |
| 5 |

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
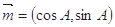 ,
, ,若
,若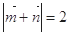
 的面积.
的面积.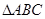 中,
中,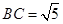 ,
,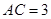 ,
,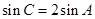 .
. 长;
长; 的值.
的值.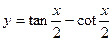 的周期为( )
的周期为( )

