题目内容
过△ABC所在平面 外一点P,作PO⊥
外一点P,作PO⊥ ,垂足为O,连接PA、PB、PC且PA、PB、PC两两垂直,则点O是△ABC的( )
,垂足为O,连接PA、PB、PC且PA、PB、PC两两垂直,则点O是△ABC的( )
A.内心 B.外心 C.垂心 D.垂心
 外一点P,作PO⊥
外一点P,作PO⊥ ,垂足为O,连接PA、PB、PC且PA、PB、PC两两垂直,则点O是△ABC的( )
,垂足为O,连接PA、PB、PC且PA、PB、PC两两垂直,则点O是△ABC的( )A.内心 B.外心 C.垂心 D.垂心
B
分析:点P为△ABC所在平面外一点,PO⊥α,垂足为O,若PA=PB=PC,可证得△POA≌△POB≌△POC,从而证得OA=OB=OC,符合这一性质的点O是△ABC外心.

证明:点P为△ABC所在平面外一点,PO⊥α,垂足为O,若PA=PB=PC,
故△POA,△POB,△POC都是直角三角形
∵PO是公共边,PA=PB=PC
∴△POA≌△POB≌△POC
∴OA=OB=OC
故O是△ABC外心
故答案为:B.

练习册系列答案
相关题目
 ,BC=2,C=
,BC=2,C= ,则边AB的长度等于_____________.
,则边AB的长度等于_____________.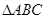 中,
中,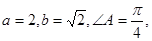 则
则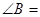 ( )
( )
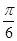
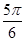
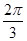
 中,若
中,若 ,则
,则 等于
等于



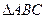 中,内角A,B,C的对边分别是
中,内角A,B,C的对边分别是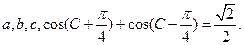
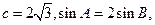 求a,b.
求a,b. 中,
中, ,则角A =
,则角A = 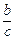 +
+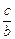 的取值范围是 .
的取值范围是 .