题目内容
已知⊿ABC的三个内角A、B、C的对边分别为a、b、c,且b2+c2=a2+bc,求:(1) 2sinBcosC-sin(B-C)的值;
(2)若a=2,求⊿ABC周长的最大值。
(2)若a=2,求⊿ABC周长的最大值。
(1);(2)6
(1)∵b2+c2=a2+bc,∴a2=b2+c2-bc,结合余弦定理知cosA=,∴A=,
∴2sinBcosC-sin(B-C)= sinBcosC+cosBsinC
=sin(B+C)
=sinA=。
(2)由a=2,结合正弦定理,得 b+c=sinB+sinC
=sinB+sin(-B)
=2sinB+2cosB=4sin(B+),
可知周长的最大值为6。
∴2sinBcosC-sin(B-C)= sinBcosC+cosBsinC
=sin(B+C)
=sinA=。
(2)由a=2,结合正弦定理,得 b+c=sinB+sinC
=sinB+sin(-B)
=2sinB+2cosB=4sin(B+),
可知周长的最大值为6。

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 且
且 ,
, 的值。
的值。 中,
中, 分别为
分别为 的对边,如果
的对边,如果 ,
, ,
, ,那么
,那么 为 ( )
为 ( )

 外一点P,作PO⊥
外一点P,作PO⊥ 、
、 、
、 ,若
,若 =
= ,则△ABC的形状为( )
,则△ABC的形状为( )
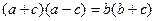 ,则
,则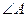 =
= 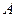 处看到河北岸
处看到河北岸
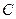 、
、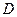 分别在东偏北
分别在东偏北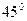 和东偏北
和东偏北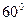 方向,此人
方向,此人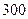 米到达
米到达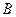 处之后,再看
处之后,再看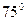 和西偏北
和西偏北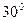 方向,求目标
方向,求目标