题目内容
已知函数 且f(1)=5.
且f(1)=5.(1)求a的值;
(2)判断函数f(x)在(2,+∞)上的单调性,并用单调性定义证明你的结论.
【答案】分析:(1)将f(1)=5代入函数解析式,列方程即可解得a的值;(2)先判断函数 在(2,+∞)上是增函数,再利用函数单调性的定义,通过作差法比较函数值的大小的方法,证明函数的单调性即可
在(2,+∞)上是增函数,再利用函数单调性的定义,通过作差法比较函数值的大小的方法,证明函数的单调性即可
解答:解:(1)∵f(1)=1+a=5
∴a=4.
(2) 在(2,+∞)上是增函数.
在(2,+∞)上是增函数.
证明:设2<x1<x2, =
= =
= ,
,
∵x1>2,x2>2,∴x1x2>4,∴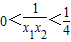 ,∴
,∴ ,
,
∴ ,
,
∴f(x1)-f(x2)<0,即f(x1)<f(x2)
∴函数f(x)在(2,+∞)上为增函数.
点评:本题考查了函数单调性的定义,利用定义证明函数的单调性的方法,作差法比较大小的技巧
 在(2,+∞)上是增函数,再利用函数单调性的定义,通过作差法比较函数值的大小的方法,证明函数的单调性即可
在(2,+∞)上是增函数,再利用函数单调性的定义,通过作差法比较函数值的大小的方法,证明函数的单调性即可解答:解:(1)∵f(1)=1+a=5
∴a=4.
(2)
 在(2,+∞)上是增函数.
在(2,+∞)上是增函数.证明:设2<x1<x2,
 =
= =
= ,
,∵x1>2,x2>2,∴x1x2>4,∴
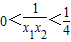 ,∴
,∴ ,
,∴
 ,
,∴f(x1)-f(x2)<0,即f(x1)<f(x2)
∴函数f(x)在(2,+∞)上为增函数.
点评:本题考查了函数单调性的定义,利用定义证明函数的单调性的方法,作差法比较大小的技巧

练习册系列答案
相关题目
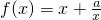 且f(1)=5.
且f(1)=5. 且f(4)=0.
且f(4)=0.