Question

1．函数f（x）=$\frac{x-2}{x+1}$在区间[1，2）上的值域为（　　）

• A． [0，$\frac{1}{2}$]
• B． [-$\frac{1}{2}$，0]
• C． （0，$\frac{1}{2}$]
• D． [-$\frac{1}{2}$，0）

Answer 1

分析 把给出的函数解析式变形，画出图形，可得f（x）=$\frac{x-2}{x+1}$在区间[1，2）上是减函数，由单调性求得函数f（x）=$\frac{x-2}{x+1}$在区间[1，2）上的值域．

解答 解：f（x）=$\frac{x-2}{x+1}$=$\frac{x+1-3}{x+1}=1-\frac{3}{x+1}$，
图象如图，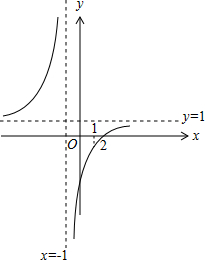

由图可知，函数f（x）=$\frac{x-2}{x+1}$在区间[1，2）上为减函数，
则值域为[-$\frac{1}{2}$，0）．
故选：D．

点评 本题考查函数的值域的求法，考查了数形结合的解题思想方法，是中档题．