题目内容
已知等比数列{an}的首项是1,公比为2,等差数列{bn}的首项是1,公差为1,把{bn}中的各项按照如下规则依次插入到{an}的每相邻两项之间,构成新数列{cn}:a1,b1,a2,b2,b3,a3,b4,b5,b6,a4,…,即在an和an+1两项之间依次插入{bn}中n个项,则c2013= .
【答案】分析:由题意可得, ,bn=1+(n-1)×1=n,当n=62时,
,bn=1+(n-1)×1=n,当n=62时, =2016即此时共有2016项,且第2016项为262,而c2013=b1951可求
=2016即此时共有2016项,且第2016项为262,而c2013=b1951可求
解答:解:由题意可得,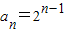 ,bn=1+(n-1)×1=n
,bn=1+(n-1)×1=n
由题意可得,在数列{an}中插入的项为,2,1,21,2,3,22,4,5,6,23…2n时,
共有项为1+2+…+n+(n+1)= =
=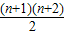
当n=62时, =2016即此时共有2016项,且第2016项为262
=2016即此时共有2016项,且第2016项为262
∴c2013=b1951=1951
故答案为:1951
点评:本题主要考查了等差数列与等比数列的通项公式的应用,解题的关键是要准确判断所求项在已知数列中所处的项的位置.
 ,bn=1+(n-1)×1=n,当n=62时,
,bn=1+(n-1)×1=n,当n=62时, =2016即此时共有2016项,且第2016项为262,而c2013=b1951可求
=2016即此时共有2016项,且第2016项为262,而c2013=b1951可求解答:解:由题意可得,
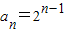 ,bn=1+(n-1)×1=n
,bn=1+(n-1)×1=n由题意可得,在数列{an}中插入的项为,2,1,21,2,3,22,4,5,6,23…2n时,
共有项为1+2+…+n+(n+1)=
 =
=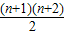
当n=62时,
 =2016即此时共有2016项,且第2016项为262
=2016即此时共有2016项,且第2016项为262∴c2013=b1951=1951
故答案为:1951
点评:本题主要考查了等差数列与等比数列的通项公式的应用,解题的关键是要准确判断所求项在已知数列中所处的项的位置.

练习册系列答案
相关题目