题目内容
下列命题中:
①“若x2+y2≠0,则x,y不全为零”的否命题;
②“若m>0,则x2+x-m=0有实根”的逆否命题;
③若过定点M(-1,0)且斜率为k的直线与圆x2+4x+y2-5=0在第一象限内的部分有交点,则k的取值范围是0≤k≤
;
④已知二面角α-l-β的平面角的大小是60°,P∈α,Q∈β,R是直线l上的任意一点,过点P与Q作直线l的垂线,垂足分别为P1,Q1,且|PP1|=2,|QQ1|=3,|P1Q1|=5,则|PR|+|QR|的最小值为5
;
以上命题正确的为______(把所有正确的命题序号写在答题卷上).
①“若x2+y2≠0,则x,y不全为零”的否命题;
②“若m>0,则x2+x-m=0有实根”的逆否命题;
③若过定点M(-1,0)且斜率为k的直线与圆x2+4x+y2-5=0在第一象限内的部分有交点,则k的取值范围是0≤k≤
| 5 |
④已知二面角α-l-β的平面角的大小是60°,P∈α,Q∈β,R是直线l上的任意一点,过点P与Q作直线l的垂线,垂足分别为P1,Q1,且|PP1|=2,|QQ1|=3,|P1Q1|=5,则|PR|+|QR|的最小值为5
| 2 |
以上命题正确的为______(把所有正确的命题序号写在答题卷上).
①“若x2+y2≠0,则x,y不全为零”的否命题是“若x2+y2=0,则x=y=0”,它是真命题;
②当m>0时,关于x的方程x2+x-m=0的判别式△=1+4m>0,
∴方程有实根,是正确的命题,
∴它的逆否命题也是正确的;
③如图,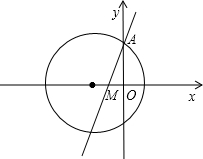 圆的方程可化为(x+2)2+y2=9,
圆的方程可化为(x+2)2+y2=9,
∴圆心坐标为(-2,0),半径r=3,
令x=0,则y=±
,
设A(0,
),又M(-1,0),∴kMA=
,
∵直线过第一象限且过(-1,0)点,∴k>0,
又直线与圆在第一象限内有交点,
∴k<
,
∴k的取值范围是(0,
);
∴命题③错误;
④如图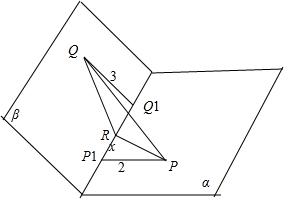 ,
,
显然,点R在P1Q1上时,|PR|+|QR|的值取到最小,
设P1R=x,则Q1R=5-x,
∴|PR|+|QR|=y=
+
(0≤x≤5),
∴当x=2时,y取得最小值5
;
∴命题④正确;
所以,以上正确的命题是①②④;
故答案为:①②④.
②当m>0时,关于x的方程x2+x-m=0的判别式△=1+4m>0,
∴方程有实根,是正确的命题,
∴它的逆否命题也是正确的;
③如图,
 圆的方程可化为(x+2)2+y2=9,
圆的方程可化为(x+2)2+y2=9,∴圆心坐标为(-2,0),半径r=3,
令x=0,则y=±
| 5 |
设A(0,
| 5 |
| 5 |
∵直线过第一象限且过(-1,0)点,∴k>0,
又直线与圆在第一象限内有交点,
∴k<
| 5 |
∴k的取值范围是(0,
| 5 |
∴命题③错误;
④如图
 ,
,显然,点R在P1Q1上时,|PR|+|QR|的值取到最小,
设P1R=x,则Q1R=5-x,
∴|PR|+|QR|=y=
| x2+22 |
| (x-5)2+32 |
∴当x=2时,y取得最小值5
| 2 |
∴命题④正确;
所以,以上正确的命题是①②④;
故答案为:①②④.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目