题目内容
动点P(x,y)是抛物线y=x2-2x-1上的点,O为坐标原点,设S=|OP|2,若x=2时,S取极小值,求S的最小值.
思路分析:本题通过建立数学模型,把实际问题转化为数学问题,然后利用函数求函数的最值.
解:S=|OP|2=x2+y2=x2+(x2-2x-1)2=x4-4x3+3x2+4x+1,
则S′=4x3-12x2+6x+4=2(x-2)(2x2-2x-1)=4(x-2)(x-![]() )(x-
)(x-![]() ).
).
令S′=0,则x1=![]() ,x2=
,x2=![]() ,x3=2.
,x3=2.
当x变化时,S′,S的变化情况如下表:
x | (-∞, |
| ( |
| ( | 2 | (2,+∞) |
S′ | - | 0 | + | 0 | - | 0 | + |
S | ?↘ | 极小值 | ?↗ | 极大值 | ↘? | 极小值 | ↗? |
∵S的定义域为(-∞,+∞),
∴所求的最小值是两个极小值中较小的一个.
∵当x=![]() 时,S=(
时,S=(![]() )4-4(
)4-4(![]() )3+3(
)3+3(![]() )2+4(
)2+4(![]() )+1=
)+1=![]() ,
,
当x=2时,S=24-4×23+3×22+4×2+1=5,
∴S的最小值为![]() .
.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
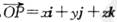 (其中i、j、k分别为X轴、y轴、z轴正方向上的单位向量).有下列命题:
(其中i、j、k分别为X轴、y轴、z轴正方向上的单位向量).有下列命题: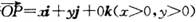 且
且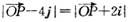 ,则
,则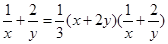
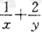 的最小值为
的最小值为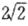 ;
;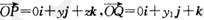 ,若向量
,若向量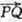 与k共线且
与k共线且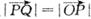 ,则动点P的轨迹是抛物线;
,则动点P的轨迹是抛物线;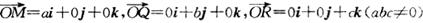 ,则平面MQR内的任意一点A (x,y,z)的坐标必然满足关系式
,则平面MQR内的任意一点A (x,y,z)的坐标必然满足关系式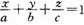 ;
;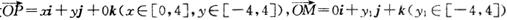 ,
,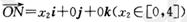 ,若向量
,若向量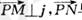 与j共线且
与j共线且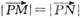 ,则动点P的轨迹是双曲线的一部分.
其中你认为正确的所有命题的序号为. _______
,则动点P的轨迹是双曲线的一部分.
其中你认为正确的所有命题的序号为. _______