题目内容
(本小题 满分12分)
满分12分)
已知:函数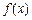 是R上的单调函数,且
是R上的单调函数,且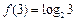 ,对于任意
,对于任意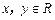 都有
都有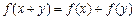 成立.
成立.
(1)求证: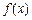 是奇函数;
是奇函数;
(2)若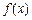 满足对任意实数
满足对任意实数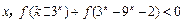 恒成立,求k的范围.
恒成立,求k的范围.
 满分12分)
满分12分) 已知:函数
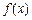 是R上的单调函数,且
是R上的单调函数,且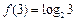 ,对于任意
,对于任意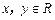 都有
都有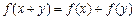 成立.
成立.(1)求证:
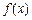 是奇函数;
是奇函数;(2)若
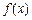 满足对任意实数
满足对任意实数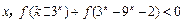 恒成立,求k的范围.
恒成立,求k的范围.(1) 证明: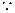
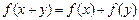
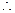 令x =" y" =" 0" 有f (0 ) = 0
令x =" y" =" 0" 有f (0 ) = 0
令y =-x 有: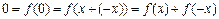 即证
即证 f ( x )是奇函
f ( x )是奇函
(2) 因为对任意实数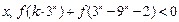 恒成立,且f ( x )是奇函数
恒成立,且f ( x )是奇函数
 恒成立又
恒成立又 R上的单调函数
R上的单调函数 f ( x )满足
f ( x )满足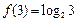 >0
>0
而f (0 ) =" 0 " 从而有:f ( x )是R上的单调增函数
于是: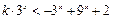
∴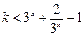 恒成立,而
恒成立,而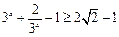
∴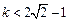
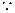
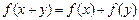
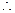 令x =" y" =" 0" 有f (0 ) = 0
令x =" y" =" 0" 有f (0 ) = 0令y =-x 有:
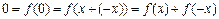 即证
即证 f ( x )是奇函
f ( x )是奇函(2) 因为对任意实数
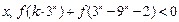 恒成立,且f ( x )是奇函数
恒成立,且f ( x )是奇函数 恒成立又
恒成立又 R上的单调函数
R上的单调函数 f ( x )满足
f ( x )满足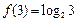 >0
>0 而f (0 ) =" 0 " 从而有:f ( x )是R上的单调增函数
于是:
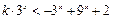
∴
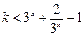 恒成立,而
恒成立,而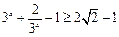
∴
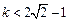
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
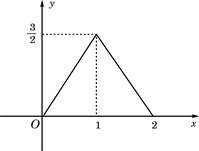
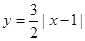 (0≤x≤2)
(0≤x≤2)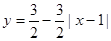 (0≤x≤2)
(0≤x≤2)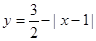 (0≤x≤2)
(0≤x≤2)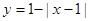 (0≤x≤2)
(0≤x≤2)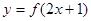 是定义在R上的奇函数,函数
是定义在R上的奇函数,函数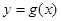 的图象与函数
的图象与函数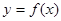 的图象关于直线
的图象关于直线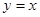 对称,则
对称,则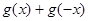 的值为
的值为 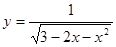 的定义域为( )
的定义域为( )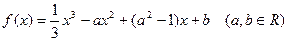 .
.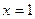 为
为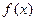 的极值点,求
的极值点,求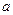 的值;
的值;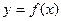 的图象在点(
的图象在点(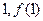 )处的切线方程为
)处的切线方程为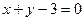 ,
,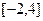 上的最大值;
上的最大值;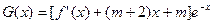 (
(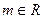 )的单调区间.
)的单调区间.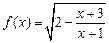 的定义域为A,不等式
的定义域为A,不等式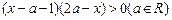 的解集为B.
的解集为B.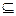 A,求实数a的取值范围.
A,求实数a的取值范围.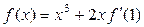 ,则
,则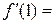 .
.