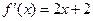题目内容
(本题满分14分)
已知函数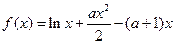 ,
,
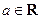 ,且
,且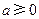 .
.
(Ⅰ)若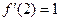 ,求
,求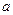 的值;
的值;
(Ⅱ)当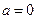 时,求函数
时,求函数 的最大值;
的最大值;
(Ⅲ)求函数 的单调递增区间.
的单调递增区间.
已知函数
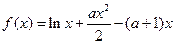 ,
,
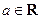 ,且
,且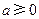 .
.(Ⅰ)若
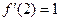 ,求
,求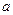 的值;
的值;(Ⅱ)当
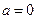 时,求函数
时,求函数 的最大值;
的最大值;(Ⅲ)求函数
 的单调递增区间.
的单调递增区间.(1)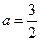 (2)
(2)
(3)当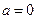 时,函数
时,函数 的递增区间是
的递增区间是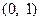 ;
;
当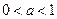 时,函数
时,函数 的递增区间是
的递增区间是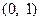 ,
, ;
;
当 时,函数
时,函数 的递增区间是
的递增区间是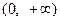 ;
;
当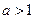 时,函数
时,函数 的递增区间是
的递增区间是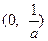 ,
,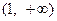 .
.
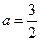 (2)
(2)
(3)当
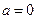 时,函数
时,函数 的递增区间是
的递增区间是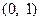 ;
;当
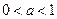 时,函数
时,函数 的递增区间是
的递增区间是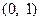 ,
, ;
;当
 时,函数
时,函数 的递增区间是
的递增区间是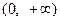 ;
;当
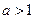 时,函数
时,函数 的递增区间是
的递增区间是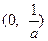 ,
,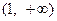 .
.(Ⅰ)函数的定义域为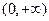 ,
,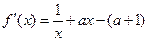 .
.
由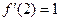 ,解得
,解得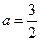 .……………………………………………………3分
.……………………………………………………3分
(Ⅱ)由 ,得
,得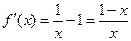 .
.
由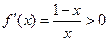 ,解得
,解得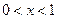 ;由
;由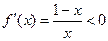 ,解得
,解得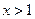 .
.
所以函数 在区间
在区间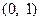 递增,
递增,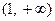 递减.
递减.
因为 是
是 在
在 上唯一一个极值点,
上唯一一个极值点,
故当 时,函数
时,函数 取得最大值,最大值
取得最大值,最大值 为
为 .…………………7分
.…………………7分
(Ⅲ)因为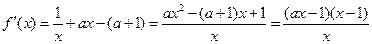
(1)当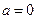 时,
时,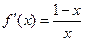 .令
.令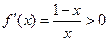 解得
解得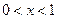
(2)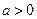 时,
时,
令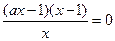 ,解得
,解得 或
或 .
.
(ⅰ)当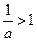 即
即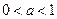 时,
时,
由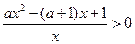 ,及
,及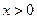 得
得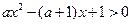 ,
,
解得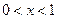 ,或
,或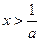 ;
;
(ⅱ)当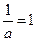 即
即 时,
时,
因为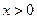 ,
,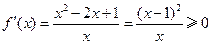 恒成立.
恒成立.
(ⅲ)当 即
即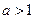 时,由
时,由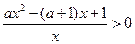 ,及
,及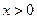 得
得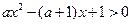 ,
,
解得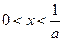 ,或
,或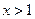 ;
;
综上所述,
当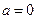 时,函数
时,函数 的递增区间是
的递增区间是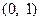 ;
;
当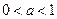 时,函数
时,函数 的递增区间是
的递增区间是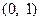 ,
, ;
;
当 时,函数
时,函数 的递增区间是
的递增区间是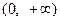 ;
;
当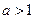 时,函数
时,函数 的递增区间是
的递增区间是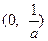 ,
,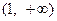 .……………………14分
.……………………14分
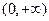 ,
,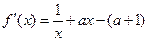 .
.由
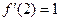 ,解得
,解得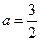 .……………………………………………………3分
.……………………………………………………3分(Ⅱ)由
 ,得
,得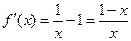 .
.由
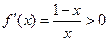 ,解得
,解得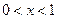 ;由
;由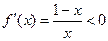 ,解得
,解得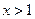 .
.所以函数
 在区间
在区间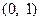 递增,
递增,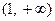 递减.
递减.因为
 是
是 在
在 上唯一一个极值点,
上唯一一个极值点,故当
 时,函数
时,函数 取得最大值,最大值
取得最大值,最大值 为
为 .…………………7分
.…………………7分(Ⅲ)因为
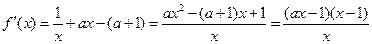
(1)当
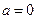 时,
时,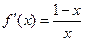 .令
.令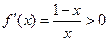 解得
解得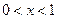
(2)
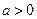 时,
时,令
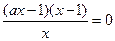 ,解得
,解得 或
或 .
.(ⅰ)当
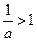 即
即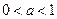 时,
时,由
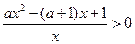 ,及
,及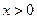 得
得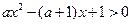 ,
,解得
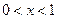 ,或
,或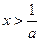 ;
;(ⅱ)当
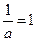 即
即 时,
时,因为
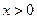 ,
,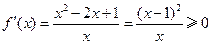 恒成立.
恒成立. (ⅲ)当
 即
即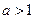 时,由
时,由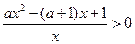 ,及
,及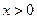 得
得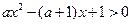 ,
,解得
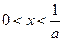 ,或
,或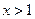 ;
;综上所述,
当
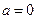 时,函数
时,函数 的递增区间是
的递增区间是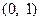 ;
;当
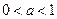 时,函数
时,函数 的递增区间是
的递增区间是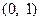 ,
, ;
;当
 时,函数
时,函数 的递增区间是
的递增区间是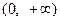 ;
;当
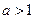 时,函数
时,函数 的递增区间是
的递增区间是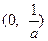 ,
,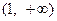 .……………………14分
.……………………14分
练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
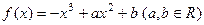 .
.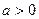 时,求函数
时,求函数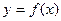 的极值;
的极值;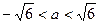 ;
;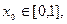
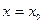 处的切线的斜率为
处的切线的斜率为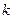 ,求证:
,求证: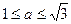 是
是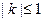 成立的充要条件.
成立的充要条件.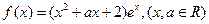 .
.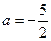 时,求函数f(x)的极小值。
时,求函数f(x)的极小值。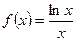 .
.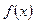 的单调性;
的单调性;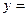
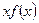 +
+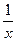 的图像总在直线
的图像总在直线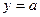 的上方,求实数
的上方,求实数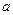 的取值范围;
的取值范围;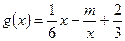 的图像有公共点,且在公共点处的切线相同,求实数
的图像有公共点,且在公共点处的切线相同,求实数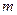 的值.
的值.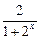 )+asinx+3(a、b为常数),若f(x)在(0,+∞)上有最大值10,则f(x)在(-∞,0)上的最小值是
)+asinx+3(a、b为常数),若f(x)在(0,+∞)上有最大值10,则f(x)在(-∞,0)上的最小值是 ,则实数a取值范围是( )
,则实数a取值范围是( )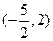
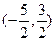
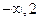 )
)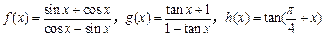 ,下列是同一函数的是( )
,下列是同一函数的是( ) 与
与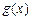
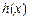
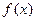 是定义在R上的偶函数,且对任意
是定义在R上的偶函数,且对任意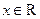 ,都有
,都有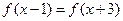 ,当
,当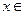 [4,6]时,
[4,6]时,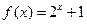 ,则函数
,则函数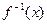 的值
的值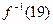 为( )
为( ) 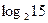
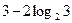
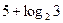
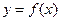 是二次函数,方程f(x)=0有两个相等的实根,且
是二次函数,方程f(x)=0有两个相等的实根,且