题目内容
如图,E为正方体ABCD-A1B1C1D1的棱AA1的中点,F为棱AB上一点,∠C1EF=90°,则
AF:FB=( )
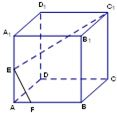
AF:FB=( )
| A.1:1 | B.1:2 | C.1:3 | D.1:4 |

设正方体的棱长为:2,由题意可知C1E=
=3,
∠C1EF=90°,所以设AF=x,12+x2+C1E2=22+22+(2-x)2
解得:x=
,所以AF:FB=
:
=1:3;
故选C.
12+(2
|
∠C1EF=90°,所以设AF=x,12+x2+C1E2=22+22+(2-x)2
解得:x=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
故选C.

练习册系列答案
相关题目
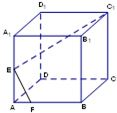 如图,E为正方体ABCD-A1B1C1D1的棱AA1的中点,F为棱AB上一点,∠C1EF=90°,则
如图,E为正方体ABCD-A1B1C1D1的棱AA1的中点,F为棱AB上一点,∠C1EF=90°,则AF:FB=( )
| A、1:1 | B、1:2 | C、1:3 | D、1:4 |
 8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )
8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )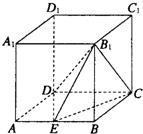 如图,已知正方体ABCD-A1B1C1D1中,E为AB的中点
如图,已知正方体ABCD-A1B1C1D1中,E为AB的中点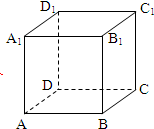 如图在正方体ABCD-A1B1C1D1中,边长为a,E为棱AB的中点.求:
如图在正方体ABCD-A1B1C1D1中,边长为a,E为棱AB的中点.求: