题目内容
19.已知函数f(x)=-$\frac{2}{3}$ax3+ax2-2x(a为实数).(1)若f(x)在R上有极值,求a的取值范围;
(2)若f(x)在[-3,-2]上是增函数,求a的取值范围.
分析 (1)求出原函数的导函数f′(x)=-2ax2+2ax-2,由f(x)在R上有极值,说明a≠0且方程-2ax2+2ax-2=0有两不等实数根,由判别式大于0求得a的取值范围;
(2)由f(x)在[-3,-2]上是增函数,可得f′(x)=-2ax2+2ax-2≥0在[-3,-2]上恒成立,分离参数a后由函数的单调性求得x2-x的范围,进一步得到
$-\frac{1}{{x}^{2}-x}$的范围,则答案可求.
解答 解:由f(x)=-$\frac{2}{3}$ax3+ax2-2x,得f′(x)=-2ax2+2ax-2.
(1)若f(x)在R上有极值,则a≠0且方程-2ax2+2ax-2=0有两不等实数根,
∴△=4a2-4×(-2a)×(-2)=4a2-16a>0,
解得:a<0或a>4;
(2)f′(x)=-2ax2+2ax-2,
要使f(x)在[-3,-2]上是增函数,则
f′(x)=-2ax2+2ax-2≥0在[-3,-2]上恒成立,
即a(x2-x)≤-1恒成立.
当x∈[-3,-2]时,x2-x>0,
则$a≤-\frac{1}{{x}^{2}-x}$在[-3,-2]上恒成立.
令t=x2-x,
∵x∈[-3,-2],∴t∈[6,12],
∴$-\frac{1}{t}∈[-\frac{1}{6},-\frac{1}{12}]$,
则$a≤-\frac{1}{6}$.
∴a的取值范围是(-∞,-$\frac{1}{6}$].
点评 本题考查利用导数研究函数的单调性,考查了利用导数求函数的最值,考查了函数恒成立问题,训练了利用分离参数法求字母的取值范围,是中高档题.

练习册系列答案
相关题目
7.有两项调查:①某社区有300个家庭,其中高收入家庭105户,中等收入家庭180户,低收入家庭15户,为了了解社会购买力的某项指标,要从中抽出一个容量为100户的样本;②在某地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况.这两项调查宜采用的抽样方法是( )
| A. | 调查①采用系统抽样法,调查②采用分层抽样法 | |
| B. | 调查①采用分层抽样法,调查②采用系统抽样法 | |
| C. | 调查①采用分层抽样法,调查②采用抽签法 | |
| D. | 调查①采用抽签法,调查②采用系统抽样法 |
14.已知向量$\overrightarrow{a}$=($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$)和$\overrightarrow{b}$=(-$\sqrt{3}$,1),则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{2π}{3}$ |
11.若点P(a,b)在函数y=x2+3lnx的图象上,点Q(c,d)在函数y=x+2的图象上,则(a-c)2+(b-d)2的最小值为( )
| A. | $\sqrt{2}$ | B. | 8 | C. | 2$\sqrt{2}$ | D. | 2 |
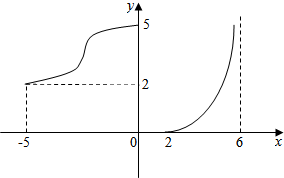 函数y=f(x)的图象如图所示
函数y=f(x)的图象如图所示