题目内容
如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径,AA1=AC=CB=2.(Ⅰ)证明:平面A1ACC1⊥平面B1BCC1;
(Ⅱ)设E,F分别为AC,BC上的动点,且CE=BF=x,问当x为何值时,三棱锥C-EC1F的体积最大,最大值为多少?

【答案】分析:(I)欲证平面A1ACC1⊥平面B1BCC1,关键是找线面垂直,根据直线与平面垂直的判定定理可知BC⊥平面A1ACC1;
(II)表示出三棱锥C-EC1F的体积,利用配方法,可得结论.
解答: (Ⅰ)证明:因为AA1⊥平面ABC,BC?平面ABC,所以AA1⊥BC,
(Ⅰ)证明:因为AA1⊥平面ABC,BC?平面ABC,所以AA1⊥BC,
因为AB是圆O直径,所以BC⊥AC,又AC∩AA1=A,所以BC⊥平面A1ACC1,
而BC?平面B1BCC1,所以平面A1ACC1⊥平面B1BCC1;
(II)解:∵CE=BF=x,∴CF=2-x
∴ =
=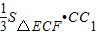 =
=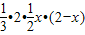 =
=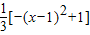
∴x=1时,三棱锥C-EC1F的体积最大,最大值为 .
.
点评:本题考查了线面、面面垂直的判定与性质定理,三棱柱的体积公式,考查学生的计算能力,属于中档题.
(II)表示出三棱锥C-EC1F的体积,利用配方法,可得结论.
解答:
 (Ⅰ)证明:因为AA1⊥平面ABC,BC?平面ABC,所以AA1⊥BC,
(Ⅰ)证明:因为AA1⊥平面ABC,BC?平面ABC,所以AA1⊥BC,因为AB是圆O直径,所以BC⊥AC,又AC∩AA1=A,所以BC⊥平面A1ACC1,
而BC?平面B1BCC1,所以平面A1ACC1⊥平面B1BCC1;
(II)解:∵CE=BF=x,∴CF=2-x
∴
 =
=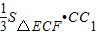 =
=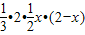 =
=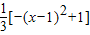
∴x=1时,三棱锥C-EC1F的体积最大,最大值为
 .
.点评:本题考查了线面、面面垂直的判定与性质定理,三棱柱的体积公式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径.
如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径. 如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径.
如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径. 如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径,AA1=AC=CB=2.
如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径,AA1=AC=CB=2.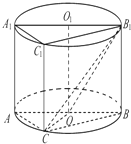 如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径.
如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O的直径.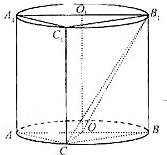 如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径.
如图,圆柱OO1内有一个三棱柱ABC-A1B1C1,三棱柱的底面为圆柱底面的内接三角形,且AB是圆O直径.