��Ŀ����
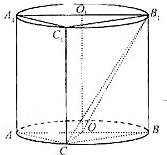 ��ͼ��Բ��OO1����һ��������ABC-A1B1C1���������ĵ���ΪԲ��������ڽ������Σ���AB��ԲOֱ����
��ͼ��Բ��OO1����һ��������ABC-A1B1C1���������ĵ���ΪԲ��������ڽ������Σ���AB��ԲOֱ������I��֤����ƽ��A1ACC1��ƽ��B1BCC1��
������AB=AA1����Բ��OO1�����ѡȡһ�㣬�Ǹõ�ȡ����������ABC-A1B1C1�ڵĸ���ΪP��
��i������C��Բ�����˶�ʱ����P�����ֵ��
��ii����ƽ��A1ACC1��ƽ��B1OC���ɵĽ�Ϊ�ȣ�0��ܦȡ�90�㣩����Pȡ���ֵʱ����cos�ȵ�ֵ��
��������I����֤ƽ��A1ACC1��ƽ��B1BCC1���ؼ��������洹ֱ������ֱ����ƽ�洹ֱ���ж�������֪BC��ƽ��A1ACC1��
����i������AC2+BC2=AB2Ϊ��ֵ�����V1�����ֵ���Ӷ��õ�p=
�����ֵ��
��ii��pȡ���ֵʱ��OC��AB��������OΪ����ԭ�㣬�����ռ�ֱ������ϵO-xyz�����ƽ��A1ACC1��һ����������ƽ��B1OC��һ����������Ȼ��������������ļнǴӶ��õ�����ǵ�����ֵ��
����i������AC2+BC2=AB2Ϊ��ֵ�����V1�����ֵ���Ӷ��õ�p=
| V1 |
| V |
��ii��pȡ���ֵʱ��OC��AB��������OΪ����ԭ�㣬�����ռ�ֱ������ϵO-xyz�����ƽ��A1ACC1��һ����������ƽ��B1OC��һ����������Ȼ��������������ļнǴӶ��õ�����ǵ�����ֵ��
����⣺������ΪAA1��ƽ��ABC��BC?ƽ��ABC������AA1��BC��
��ΪAB��ԲOֱ��������BC��AC����AC��AA1=A������BC��ƽ��A1ACC1��
��BC?ƽ��B1BCC1������ƽ��A1ACC1��ƽ��B1BCC1��
����i����Բ���ĵ���뾶Ϊr����AB=AA1=2r��
��������ABC-A1B1C1�����Ϊ V1=
AC•BC•2r=AC•BC•r��
����ΪAC2+BC2=AB2=4r2��
���� AC•BC��
=2r2�����ҽ��� AC=BC=
rʱ�Ⱥų�����
�Ӷ�V1��2r3����Բ�������V=��r2•2r=2��r3��
��p=
��
=
��
���ҽ��� AC=BC=
r����OC��ABʱ�Ⱥų�����
����p�����ֵ��
��
��ii��pȡ���ֵʱ��OC��AB��
������OΪ����ԭ�㣬
�����ռ�ֱ������ϵO-xyz��
��C��r��0��0����B��0��r��0����B1��0��r��2r����
��ΪBC��ƽ��A1ACC1��
����
=(r��-r��0)��ƽ��A1ACC1��һ����������
��ƽ��B1OC�ķ�����
=(x��y��z)��
��
��
��
��
��
ȡz=1��ƽ��B1OC��һ��������Ϊ
=(0��-2��1)��
��Ϊ0�㣼�ȡ�90�㣬
���� cos��=|cos?
��
��|
=|
|
=|
|
=
��
��ΪAB��ԲOֱ��������BC��AC����AC��AA1=A������BC��ƽ��A1ACC1��
��BC?ƽ��B1BCC1������ƽ��A1ACC1��ƽ��B1BCC1��
����i����Բ���ĵ���뾶Ϊr����AB=AA1=2r��
��������ABC-A1B1C1�����Ϊ V1=
| 1 |
| 2 |
����ΪAC2+BC2=AB2=4r2��
���� AC•BC��
| AC2+BC2 |
| 2 |
| 2 |
�Ӷ�V1��2r3����Բ�������V=��r2•2r=2��r3��
��p=
| V1 |
| V |
| 2r3 |
| 2��r3 |
| 1 |
| �� |
���ҽ��� AC=BC=
| 2 |
����p�����ֵ��
| 1 |
| �� |
��ii��pȡ���ֵʱ��OC��AB��
������OΪ����ԭ�㣬
�����ռ�ֱ������ϵO-xyz��
��C��r��0��0����B��0��r��0����B1��0��r��2r����
��ΪBC��ƽ��A1ACC1��
����
| BC |
��ƽ��B1OC�ķ�����
| n |
��
|
|
��
|
ȡz=1��ƽ��B1OC��һ��������Ϊ
| n |
��Ϊ0�㣼�ȡ�90�㣬
���� cos��=|cos?
| n |
| BC |
=|
| ||||
|
|
=|
| 2r | ||||
|
=
| ||
| 5 |
��������С����Ҫ����ֱ����ֱ�ߡ�ֱ����ƽ�桢ƽ����ƽ���λ�ù�ϵ���Լ����������������θ��͵Ȼ���֪ʶ������ռ������������������������������֤�������������ν��˼�롢������ת��˼�롢��Ȼ���Ȼ˼�룮

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ��Բ��OO1����һ��������ABC-A1B1C1���������ĵ���ΪԲ��������ڽ������Σ���AB��ԲO��ֱ����
��ͼ��Բ��OO1����һ��������ABC-A1B1C1���������ĵ���ΪԲ��������ڽ������Σ���AB��ԲO��ֱ���� ��ͼ��Բ��OO1����һ��������ABC-A1B1C1���������ĵ���ΪԲ��������ڽ������Σ���AB��ԲO��ֱ����
��ͼ��Բ��OO1����һ��������ABC-A1B1C1���������ĵ���ΪԲ��������ڽ������Σ���AB��ԲO��ֱ���� ��ͼ��Բ��OO1����һ��������ABC-A1B1C1���������ĵ���ΪԲ��������ڽ������Σ���AB��ԲOֱ����AA1=AC=CB=2��
��ͼ��Բ��OO1����һ��������ABC-A1B1C1���������ĵ���ΪԲ��������ڽ������Σ���AB��ԲOֱ����AA1=AC=CB=2��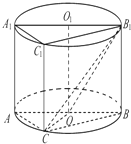 ��ͼ��Բ��OO1����һ��������ABC-A1B1C1���������ĵ���ΪԲ��������ڽ������Σ���AB��ԲO��ֱ����
��ͼ��Բ��OO1����һ��������ABC-A1B1C1���������ĵ���ΪԲ��������ڽ������Σ���AB��ԲO��ֱ����