题目内容
函数y=esin x(-π≤x≤π)的大致图象为 ( ).
D
解析试题分析:取x=-π,0,π这三个值,可得y总是1,故排除A、C;当0<x< 时,sin x是增函数,ex也是增函数,故y=esin x也是增函数,故选D.
时,sin x是增函数,ex也是增函数,故y=esin x也是增函数,故选D.
考点:复合函数的单调性;指数函数的性质;正弦函数的性质;函数的图像。
点评:我们判断函数的图像,一般可以根据函数的定义域、值域、奇偶性、单调性、特殊值或特殊点进行判断。

练习册系列答案
相关题目
已知 是定义在R上的奇函数,若对于x≥0,都有f(x+2)=
是定义在R上的奇函数,若对于x≥0,都有f(x+2)= ,且当
,且当 时,
时, ,则
,则 =
=
| A.1-e | B.e-1. | C.-l-e | D.e+l |
函数 的反函数的图象过
的反函数的图象过 点,则
点,则 的值为( )
的值为( )
A. | B. | C. 或 或 | D. |
已知 , 四个函数中,当
, 四个函数中,当 时, 满足不等式
时, 满足不等式 的是
的是
A. | B. |
C. | D. |
设定义在 上的奇函数
上的奇函数 ,满足对任意
,满足对任意 都有
都有 ,且
,且 时,
时, ,则
,则 的值等于( )
的值等于( )
A. | B. | C. | D. |
下列函数中,在 上为增函数的是 ( )
上为增函数的是 ( )
A. | B. | C. | D. |
函数
 的部分图象如图所示,则
的部分图象如图所示,则 ( )
( )
A. | B.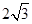 | C. | D. |
函数, 的定义域为
的定义域为
A. | B. | C. | D. |
若方程 的根在区间
的根在区间 上,则
上,则 的值为( )
的值为( )
A. | B.1 | C. 或2 或2 | D. 或1 或1 |