题目内容
若方程 的根在区间
的根在区间 上,则
上,则 的值为( )
的值为( )
A. | B.1 | C. 或2 或2 | D. 或1 或1 |
D
解析试题分析:令f(x)= ,且x>-1,则方程
,且x>-1,则方程 的实数根即为f(x)的零点.
的实数根即为f(x)的零点.
则当x>0时,f(x)在区间(k,k+1)(k∈Z)上单调递增,
由于f(1)=ln2-2<0,f(2)=ln3-1>0,
∴f(1)•f(2)<0,故f(x)在(1,2)上有唯一零点.
当x<0时,f(x)在区(-1,0)上也是增函数,由f(- )=ln
)=ln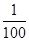 +
+ =
= -ln100<3-lne3=0,
-ln100<3-lne3=0,
f(-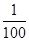 )=ln
)=ln +200>200-ln1>200>0,
+200>200-ln1>200>0,
可得 f(- )•f(-
)•f(-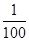 )<0,故函数f(x)在(-
)<0,故函数f(x)在(- ,-
,-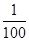 )上也有唯一零点,
)上也有唯一零点,
故f(x)在区(-1,0)上也唯一零点,此时,k=-1.
综上可得,∴k=±1,故选D.
考点:函数的零点的定义,零点存在定理。
点评:中档题,判断函数的零点所在的区间的方法,主要是零点存在定理。本题解答体现了化归与转化、分类讨论的数学思想。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列函数中,既是偶函数,又在 上单调递增的函数是 ( )
上单调递增的函数是 ( )
A. | B.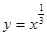 | C. | D. |
函数f(x)=ax2+2(a-1)x+2在区间(-∞,4)上为减函数,则a的取值范围为( )
A.0<a≤ | B.0≤a≤ | C.0<a≤ | D.a> |
已知不等式 对任意
对任意 及
及 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
已知函数 的图象如图所示,将
的图象如图所示,将 的图象向左平移
的图象向左平移 个单位,得到
个单位,得到 的图象,则函数
的图象,则函数 的解析式为( )
的解析式为( )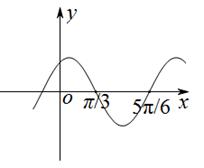
A. | B. |
C. | D. |
已知f(x)=x3+x,若a,b,c∈R,且a+b>0,a+c>0,b+c>0,则f(a)+f(b)+f(c)的值( )
| A.一定大于0 | B.一定等于0 | C.一定小于0 | D.正负都有可能 |


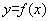 的值域是
的值域是 ,则函数
,则函数 的值域是( )
的值域是( )