题目内容
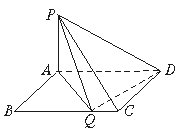
如图,矩形ABCD中,|AB|=1,|BC|=a,PA⊥面ABCD且|PA|=1.
(1)BC边上是否存在点Q,使得PQ⊥QD,并说明理由;
(2)若BC边上存在唯一的点Q使得PQ⊥QD,指出点Q的位置,并求出此时AD与平面PDQ所成的角的正弦值;
(3)在(2)的条件下,求二面角Q—PD—A的正弦值.
答案:
解析:
提示:
解析:
|
当a≥2时才存在; |
提示:
|
(1)若BC边上存在点Q,使PQ⊥QD,因PA⊥面ABCD知AQ⊥QD.矩形ABCD中,当a<2时,直线BC与以AD为直径的圆相离,故不存在点Q使AQ⊥QD,故仅当a≥2时才存在点Q使PQ⊥QD; (2)当a=2时,以AD为直径的圆与BC相切于Q,此时Q是唯一的点使∠AQD为直角,且Q为BC的中点.作AH⊥PQ于H,可证∠ADH为AD与平面PDQ所成的角,且在Rt△PAQ中可求得sinADH= (3)作AG⊥PD于G,可证∠AGH为二面角Q—PD—A的平面角,且在Rt△PAD中可求得sinAGH= |

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
 如图,矩形ABCD中,AB=
如图,矩形ABCD中,AB=
 A 若方程ax-x-a=0有两个实数解,则a的取值范围是
A 若方程ax-x-a=0有两个实数解,则a的取值范围是 如图,矩形ABCD中,
如图,矩形ABCD中, (理)如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD
(理)如图,矩形ABCD中,AB=1,BC=a,PA⊥平面ABCD