题目内容
设全集U=R,函数f(x)=lg(|x+1|+a-1)(a<1)的定义域为A,集合B={x|cosπx=1}.若(∁UA)∩B恰好有2个元素,求a的取值集合.
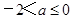
|x+1|+a-1>0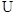 ?|x+1|>1-a,
?|x+1|>1-a,
当a<1时,1-a>0,∴x>-a或x<a-2,
∴A=(-∞,a-2)∪(-a,+∞).
∵cosπx=1,∴πx=2kπ,∴x=2k(k∈Z),
∴B={x|x=2k,k∈Z}.
当a<1时,∁UA=[a-2,-a]在此区间上恰有2个偶数.
∴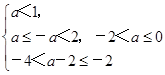 .
.
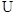 ?|x+1|>1-a,
?|x+1|>1-a,当a<1时,1-a>0,∴x>-a或x<a-2,
∴A=(-∞,a-2)∪(-a,+∞).
∵cosπx=1,∴πx=2kπ,∴x=2k(k∈Z),
∴B={x|x=2k,k∈Z}.
当a<1时,∁UA=[a-2,-a]在此区间上恰有2个偶数.
∴
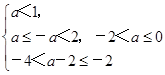 .
.
练习册系列答案
 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案
相关题目
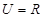 ,集合
,集合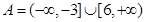 ,
,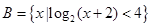 .
.
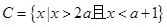 ,若
,若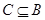 ,求实数
,求实数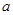 的取值范围.
的取值范围.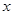 的二次方程
的二次方程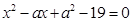 和
和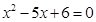 的解集分别是集合
的解集分别是集合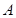 和
和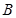 ,若
,若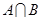 为单元素集,求
为单元素集,求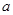 的值.
的值.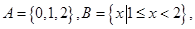 则
则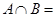 ( )
( )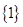
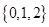
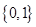
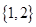
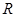 表示实数集,集合
表示实数集,集合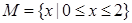 ,
,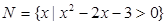 ,则下列结论正确的是( )
,则下列结论正确的是( )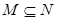
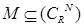
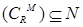
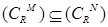
 ,
, ,则
,则 ( )
( )



 ,
, ,,则
,,则 ( )
( )


