题目内容
设函数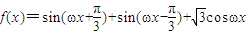 (其中ω>0),且函数f(x)图象的两条相邻的对称轴间的距离为
(其中ω>0),且函数f(x)图象的两条相邻的对称轴间的距离为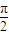 .
.(1)求ω的值;
(2)将函数y=f(x)的图象上各点横坐标伸长到原来的2倍,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在区间
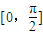 的最大值和最小值.
的最大值和最小值.
【答案】分析:(1)利用两角和的正弦公式化简函数f(x)的解析式为 ,再根据周期求得ω的值.
,再根据周期求得ω的值.
(2)由(1)得f(x)=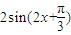 ,再根据函数y=Asin(ωx+φ)的图象变换规律求得g(x)=
,再根据函数y=Asin(ωx+φ)的图象变换规律求得g(x)=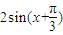 ,由x∈
,由x∈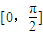 ,根据正弦函数的定义域和值域求得函数g(x)在区间
,根据正弦函数的定义域和值域求得函数g(x)在区间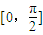 的最大值和最小值.
的最大值和最小值.
解答:解:(1)由于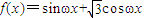 =
=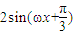 .…(3分)
.…(3分)
∵函数f(x)图象的两条相邻的对称轴间的距离为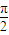 ,∴
,∴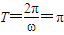 .…(5分)
.…(5分)
∴ω=2.…(6分)
(2)由(1)得f(x)=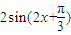 ,∴g(x)=
,∴g(x)=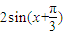 .…(8分)
.…(8分)
由x∈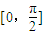 可得
可得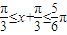 ,…(10分)
,…(10分)
∴当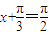 ,即x=
,即x=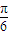 时,g(x)取得最大值为
时,g(x)取得最大值为 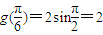 ;
;
当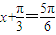 ,即x=
,即x=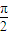 时,g(x)取得最小值为
时,g(x)取得最小值为 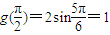 .…(12分)
.…(12分)
点评:本题主要考查两角和的正弦公式,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的周期性、定义域和值域,属于中档题.
 ,再根据周期求得ω的值.
,再根据周期求得ω的值.(2)由(1)得f(x)=
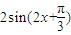 ,再根据函数y=Asin(ωx+φ)的图象变换规律求得g(x)=
,再根据函数y=Asin(ωx+φ)的图象变换规律求得g(x)=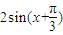 ,由x∈
,由x∈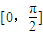 ,根据正弦函数的定义域和值域求得函数g(x)在区间
,根据正弦函数的定义域和值域求得函数g(x)在区间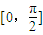 的最大值和最小值.
的最大值和最小值.解答:解:(1)由于
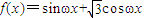 =
=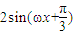 .…(3分)
.…(3分)∵函数f(x)图象的两条相邻的对称轴间的距离为
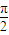 ,∴
,∴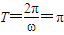 .…(5分)
.…(5分)∴ω=2.…(6分)
(2)由(1)得f(x)=
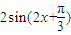 ,∴g(x)=
,∴g(x)=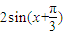 .…(8分)
.…(8分)由x∈
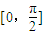 可得
可得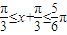 ,…(10分)
,…(10分)∴当
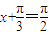 ,即x=
,即x=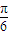 时,g(x)取得最大值为
时,g(x)取得最大值为 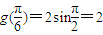 ;
;当
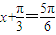 ,即x=
,即x=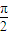 时,g(x)取得最小值为
时,g(x)取得最小值为 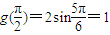 .…(12分)
.…(12分)点评:本题主要考查两角和的正弦公式,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的周期性、定义域和值域,属于中档题.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
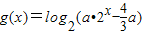 ,其中a>0.若函数f(x)与g(x)的图象有且只有一个交点,求a的取值范围.
,其中a>0.若函数f(x)与g(x)的图象有且只有一个交点,求a的取值范围. ,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2. (其中常数
(其中常数 >0,且
>0,且 时,解关于
时,解关于 的方程
的方程 (其中常数
(其中常数 );
); 在
在 上的最小值是一个与
上的最小值是一个与