题目内容
设函数 ,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.(1)求函数f(x)的表达式;
(2)若方程f(x)=x+a(a∈R)至少有两个零点,求实数a取值的集合.
【答案】分析:(1)由题意,当且仅当x=-2时,函数f(x)取得最小值-2,即为二次函数当x=-2时,函数f(x)取得最小值-2,从而利用二次函数求最值的方法可求;
(2)由题意,方程可化为x2+3x+2-a=0,要使方程有两不等实根,则判别式=9-4(2-a)>0,解不等式可求.
解答:解:(1)由于二次函数的对称轴为x=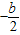 此时有最小值
此时有最小值
即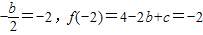
解得b=4,c=2
所以f(x)=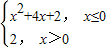 ,
,
(2)由题意,方程可化为x2+3x+2-a=0
要使方程有两不等实根,则判别式=9-4(2-a)>0
解得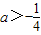
∴a取值范围的集合为{a|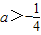 }
}
点评:本题的考点是函数的零点与方程根的关系,主要考查函数解析式的求解,考查函数的零点与方程根的关系,关键是将问题转化为对应方程根的问题.
(2)由题意,方程可化为x2+3x+2-a=0,要使方程有两不等实根,则判别式=9-4(2-a)>0,解不等式可求.
解答:解:(1)由于二次函数的对称轴为x=
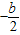 此时有最小值
此时有最小值即
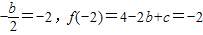
解得b=4,c=2
所以f(x)=
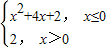 ,
,(2)由题意,方程可化为x2+3x+2-a=0
要使方程有两不等实根,则判别式=9-4(2-a)>0
解得
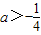
∴a取值范围的集合为{a|
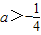 }
}点评:本题的考点是函数的零点与方程根的关系,主要考查函数解析式的求解,考查函数的零点与方程根的关系,关键是将问题转化为对应方程根的问题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
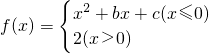 ,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2. ,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2. ,其中b为实数。
,其中b为实数。 ,其中b为实数.
,其中b为实数.