题目内容
设函数ω(其中A>0,ω>0,-π<φ<π )在x=
处取得最大值2,其图象与轴的相邻两个交点的距离为
.
(I)求f(x)的解析式;
(II)求函数f(x)的值域.
| π |
| 6 |
| π |
| 2 |
(I)求f(x)的解析式;
(II)求函数f(x)的值域.
(Ⅰ)由题意可知f(x)的周期为T=π,即
=π,解得ω=2.
因此f(x)在x=
处取得最大值2,所以A=2,从而sin(2×
+φ)=1,
所以
+φ=
+2kπ,k∈z,又-π<φ≤π,得φ=
,
故f(x)的解析式为f(x)=2sin(2x+
);
(Ⅱ)因为y=sinx∈[-1,1],
所以sin(2x+
)∈[-1,1];则2sin(2x+
)∈[-2,2];
函数f(x)的值域:[-2,2]
| 2π |
| ω |
因此f(x)在x=
| π |
| 6 |
| π |
| 6 |
所以
| π |
| 3 |
| π |
| 2 |
| π |
| 6 |
故f(x)的解析式为f(x)=2sin(2x+
| π |
| 6 |
(Ⅱ)因为y=sinx∈[-1,1],
所以sin(2x+
| π |
| 6 |
| π |
| 6 |
函数f(x)的值域:[-2,2]

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
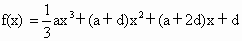 ,
,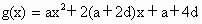 ,其中a>0,d>0,设
,其中a>0,d>0,设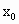 为f(x)的极小值点,
为f(x)的极小值点,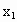 为g(x)的极值点,
为g(x)的极值点,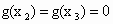 ,并且
,并且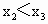 ,将点(
,将点(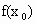 ),(
),(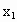 ,
,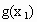 ),(
),(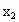 ,0),(
,0),(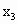 ,0)依次记为A,B,C,D.
,0)依次记为A,B,C,D.