题目内容
【题目】已知圆![]() 的圆心
的圆心![]() 在
在![]() 轴的正半轴上,半径为2,且被直线
轴的正半轴上,半径为2,且被直线![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求圆![]() 的方程;
的方程;
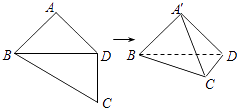
(2)设![]() 是直线
是直线![]() 上的动点,过点
上的动点,过点![]() 作圆
作圆![]() 的切线
的切线![]() ,切点为
,切点为![]() ,证明:经过
,证明:经过![]() ,
,![]() ,
,![]() 三点的圆必过定点,并求出所有定点的坐标.
三点的圆必过定点,并求出所有定点的坐标.
【答案】(1) 圆![]() :
:![]() . (2)证明见解析;
. (2)证明见解析;![]() ,
,![]() .
.
【解析】
(1)设出圆心坐标,利用点到直线距离公式以及圆的弦长列方程,解方程求得圆心坐标,进而求得圆![]() 的方程.(2)设出
的方程.(2)设出![]() 点坐标,根据过圆的切线的几何性质,得到过
点坐标,根据过圆的切线的几何性质,得到过![]() ,
,![]() ,
,![]() 三点的圆是以
三点的圆是以![]() 为直径的圆.设出圆上任意一点
为直径的圆.设出圆上任意一点![]() 的坐标,利用
的坐标,利用![]() ,结合向量数量积的坐标运算进行化简,得到该圆对应的方程
,结合向量数量积的坐标运算进行化简,得到该圆对应的方程![]() ,根据方程过的定点与
,根据方程过的定点与![]() 无关列方程组,解方程组求得该圆所过定点.
无关列方程组,解方程组求得该圆所过定点.
解:(1)设圆心![]() ,
,
则圆心![]() 到直线
到直线![]() 的距离
的距离![]() .
.
因为圆被直线![]() 截得的弦长为
截得的弦长为![]()
∴![]() .
.
解得![]() 或
或![]() (舍),∴圆
(舍),∴圆![]() :
:![]() .
.
(2)已知![]() ,设
,设![]() ,
,
∵![]() 为切线,∴
为切线,∴![]() ,∴过
,∴过![]() ,
,![]() ,
,![]() 三点的圆是以
三点的圆是以![]() 为直径的圆.
为直径的圆.
设圆上任一点为![]() ,则
,则![]() .
.
∵![]() ,
,![]() ,∴
,∴![]()
即![]() .
.
若过定点,即定点与![]() 无关
无关
令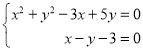
解得![]() 或
或![]() ,所以定点为
,所以定点为![]() ,
,![]() .
.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目