题目内容
下列函数中周期是2的函数是
①y=2cos2πx-1②y=sinπx+cosπx③y=tan(
x+
)④y=sinπxcosπx.
②③
②③
①y=2cos2πx-1②y=sinπx+cosπx③y=tan(
| π |
| 2 |
| π |
| 3 |
分析:利用二倍角公式,和角的三角函数公式分别化简,再利用周期公式可求.
解答:解:对于①y=cos2πx,∴T=
=1;
对于②y=
sin(πx+
),∴T=
=2;
对于③T=
=2;
对于④y=
sin2πx,∴T=
=1;
故答案为②③
| 2π |
| 2π |
对于②y=
| 2 |
| π |
| 4 |
| 2π |
| π |
对于③T=
| π | ||
|
对于④y=
| 1 |
| 2 |
| 2π |
| 2π |
故答案为②③
点评:本题主要考查三角函数的最小正周期的求法,一般先将函数化简为y=Asin(wx+ρ)的形式,再由最小正周期的求法T=
解题.
| 2π |
| w |

练习册系列答案
相关题目
下列函数中周期是2的函数是( )
| A、y=2cos2πx-1 | ||||
| B、y=sin2πx+cosπx | ||||
C、y=tan(
| ||||
| D、y=sinπxcosπx |
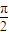 x+
x+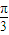 )
)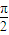 x+
x+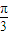 )
)