题目内容
下列函数中周期是2的函数是( )A.y=2cos2πx-1
B.y=sin2πx+cosπ
C.y=tan(
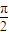 x+
x+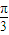 )
)D.y=sinπxcosπ
【答案】分析:分别对4个选项进行化简,求出各自周期,然后与已知要求周期比较即可排除选项.
解答:解:A:y=2cos2πx-1即:y=cos2πx,故周期为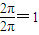 ,∴排除A.
,∴排除A.
B:y=sin2πx+cosπx,∵y=sin2πx周期为1,y=cosπx周期为2,故排除B.
C:y=tan(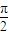 x+
x+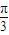 ),T=
),T= ,C正确.
,C正确.
D:y=sinπxcosπx,即y=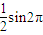 ,T=1.故排除D.
,T=1.故排除D.
故选:C.
点评:本题考查三角函数的周期性及其求法,需要对三角函数的定义已知转化熟练掌握,属于基础题.
解答:解:A:y=2cos2πx-1即:y=cos2πx,故周期为
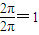 ,∴排除A.
,∴排除A.B:y=sin2πx+cosπx,∵y=sin2πx周期为1,y=cosπx周期为2,故排除B.
C:y=tan(
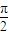 x+
x+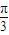 ),T=
),T= ,C正确.
,C正确.D:y=sinπxcosπx,即y=
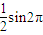 ,T=1.故排除D.
,T=1.故排除D.故选:C.
点评:本题考查三角函数的周期性及其求法,需要对三角函数的定义已知转化熟练掌握,属于基础题.

练习册系列答案
相关题目
下列函数中周期是2的函数是( )
| A、y=2cos2πx-1 | ||||
| B、y=sin2πx+cosπx | ||||
C、y=tan(
| ||||
| D、y=sinπxcosπx |
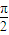 x+
x+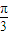 )
)