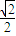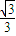题目内容
过椭圆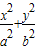
=1（a＞b＞0）右焦点F（2，0）作倾斜角为60°的直线，与椭圆交于A、B两点，若|BF|=2|AF|，则椭圆的离心率为（ ）A．
B．
C．
D．
【答案】分析：由直线方程的点斜式，可得直线AB的方程为y=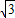
（x-2），与椭圆的方程消去x，得（a2+
b2）y2+
b2y+4b2-a2b2=0．设A（x1，y1），B（x2，y2），由根与系数的关系结合已知条件得y1+y2=-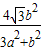
=-y1，y1y2=
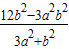=-2y12，消去y1得关于a、b的方程，结合a2=b2+4联解，可得a=3，从而得到该椭圆的离心率．
解答：解：∵直线AB经过F（2，0）且倾斜角为60°，
∴AB的斜率k=tan60°=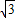
，得直线AB方程为y=
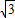（x-2）
将直线AB方程与椭圆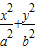
=1联解，消去x得：（a2+
b2）y2+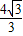
b2y+4b2-a2b2=0
设A（x1，y1），B（x2，y2），得y1+y2=-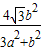
，y1y2=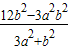
∵|BF|=2|AF|，
∴y1+y2=-y1=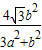
，y1y2=-2y12=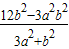
消去y1，得-2（
）2=
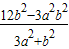…（1）
又∵椭圆的焦点F（2，0）
∴a2=b2+4，代入（1）式化简整理，得-96b4=-3b4（4b2+12），解之得b2=5
由此可得a2=9，a=3，所以椭圆的离心率e=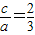
故选：B
点评：本题给出椭圆经过右焦点倾角为60度的弦AB被焦点分成1：2的两部分，求椭圆的离心率，着重考查了椭圆的几何性质、直线与椭圆的位置关系等知识点，属于基础题．
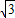（x-2），与椭圆的方程消去x，得（a2+b2）y2+b2y+4b2-a2b2=0．设A（x1，y1），B（x2，y2），由根与系数的关系结合已知条件得y1+y2=-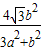=-y1，y1y2=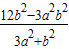=-2y12，消去y1得关于a、b的方程，结合a2=b2+4联解，可得a=3，从而得到该椭圆的离心率．解答：解：∵直线AB经过F（2，0）且倾斜角为60°，
∴AB的斜率k=tan60°=
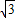，得直线AB方程为y=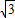（x-2）将直线AB方程与椭圆
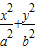=1联解，消去x得：（a2+b2）y2+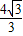b2y+4b2-a2b2=0设A（x1，y1），B（x2，y2），得y1+y2=-
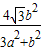，y1y2=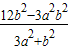∵|BF|=2|AF|，
∴y1+y2=-y1=
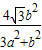，y1y2=-2y12=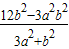消去y1，得-2（
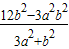）2=…（1）又∵椭圆的焦点F（2，0）
∴a2=b2+4，代入（1）式化简整理，得-96b4=-3b4（4b2+12），解之得b2=5
由此可得a2=9，a=3，所以椭圆的离心率e=
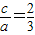
故选：B
点评：本题给出椭圆经过右焦点倾角为60度的弦AB被焦点分成1：2的两部分，求椭圆的离心率，着重考查了椭圆的几何性质、直线与椭圆的位置关系等知识点，属于基础题．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
+
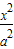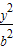=1（a＞b＞0）的左焦点F1作x轴的垂线交椭圆于点P，F2为右焦点，若∠F1PF2=60°，则椭圆的离心率为（ ）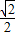
+
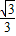
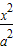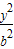=1（a＞b＞0）的右焦点的弦为直径的圆与其右准线的位置关系是（ ）
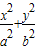=1（a＞b＞0）的左焦点F任作一条与两坐标轴都不垂直的弦AB；若点M在x轴上，且使得MF为△AMB的一条内角平分线，则称点M为该椭圆的“左特征点”．
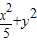=1的“左特征点”M的坐标．
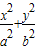=1（a＞b＞0）的“左特征点”M是一个怎么样的点？并证明你的结论．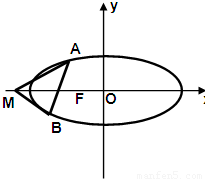
+
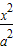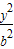=1（a＞b＞0）的左焦点F1作x轴的垂线交椭圆于点P，F2为右焦点，若∠F1PF2=60°，则椭圆的离心率为（ ）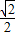
+
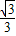
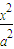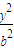=1（a＞b＞0）的左焦点F1作x轴的垂线交椭圆于点P，F2为右焦点，若∠F1PF2=60°，则椭圆的离心率为（ ）
