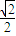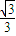题目内容
过椭圆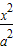 +
+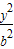 =1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )
=1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )A.
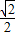
B.
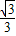
C.

D.

【答案】分析:把x=-c代入椭圆方程求得P的坐标,进而根据∠F1PF2=60°推断出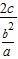 =
=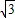 整理得
整理得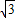 e2+2e-
e2+2e-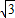 =0,进而求得椭圆的离心率e.
=0,进而求得椭圆的离心率e.
解答:解:由题意知点P的坐标为(-c,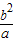 )或(-c,-
)或(-c,-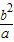 ),
),
∵∠F1PF2=60°,
∴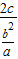 =
=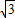 ,
,
即2ac=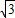 b2=
b2=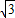 (a2-c2).
(a2-c2).
∴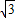 e2+2e-
e2+2e-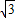 =0,
=0,
∴e=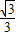 或e=-
或e=-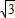 (舍去).
(舍去).
故选B.
点评:本题主要考查了椭圆的简单性质,考查了考生综合运用椭圆的基础知识和分析推理的能力.
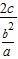 =
=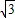 整理得
整理得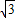 e2+2e-
e2+2e-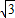 =0,进而求得椭圆的离心率e.
=0,进而求得椭圆的离心率e.解答:解:由题意知点P的坐标为(-c,
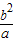 )或(-c,-
)或(-c,-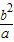 ),
),∵∠F1PF2=60°,
∴
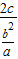 =
=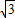 ,
,即2ac=
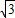 b2=
b2=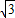 (a2-c2).
(a2-c2).∴
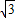 e2+2e-
e2+2e-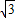 =0,
=0,∴e=
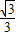 或e=-
或e=-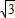 (舍去).
(舍去).故选B.
点评:本题主要考查了椭圆的简单性质,考查了考生综合运用椭圆的基础知识和分析推理的能力.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
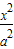 +
+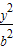 =1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )
=1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )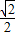
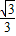


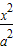 +
+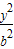 =1(a>b>0)的右焦点的弦为直径的圆与其右准线的位置关系是( )
=1(a>b>0)的右焦点的弦为直径的圆与其右准线的位置关系是( )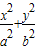 =1(a>b>0)的左焦点F任作一条与两坐标轴都不垂直的弦AB;若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.
=1(a>b>0)的左焦点F任作一条与两坐标轴都不垂直的弦AB;若点M在x轴上,且使得MF为△AMB的一条内角平分线,则称点M为该椭圆的“左特征点”.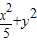 =1的“左特征点”M的坐标.
=1的“左特征点”M的坐标.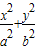 =1(a>b>0)的“左特征点”M是一个怎么样的点?并证明你的结论.
=1(a>b>0)的“左特征点”M是一个怎么样的点?并证明你的结论.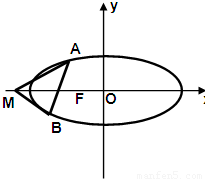
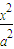 +
+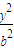 =1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )
=1(a>b>0)的左焦点F1作x轴的垂线交椭圆于点P,F2为右焦点,若∠F1PF2=60°,则椭圆的离心率为( )