题目内容
以过椭圆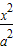
+
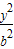=1（a＞b＞0）的右焦点的弦为直径的圆与其右准线的位置关系是（ ）A．相交
B．相切
C．相离
D．不能确定
【答案】分析：根据圆锥曲线的统一定义，可得过椭圆右焦点F的弦AB中点为M，且M到右准线l的距离大于圆的半径，由此可得该圆与右准线l的位置．
解答：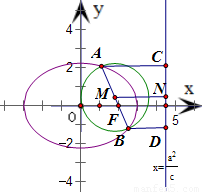
解：设过右焦点F的弦为AB，右准线为l，A、B在l上的射影分别为C、D
连接AC、BD，设AB的中点为M，作MN⊥l于N
根据圆锥曲线的统一定义，可得
=
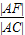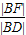=e，可得
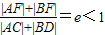
∴|AF|+|BF|＜|AC|+|BD|，即|AB|＜|AC|+|BD|，
∵以AB为直径的圆半径为r=
|AB|，|MN|=
（|AC|+|BD|）
∴圆M到l的距离|MN|＞r，可得直线l与以AB为直径的圆相离
故选：C
点评：本题给出椭圆的右焦点F，求以经过F的弦AB为直径的圆与右准线的位置关系，着重考查了椭圆的简单几何性质、圆锥曲线的统一定义和直线与圆的位置关系等知识，属于中档题．
解答：
解：设过右焦点F的弦为AB，右准线为l，A、B在l上的射影分别为C、D连接AC、BD，设AB的中点为M，作MN⊥l于N
根据圆锥曲线的统一定义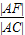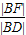，可得
==e，可得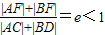∴|AF|+|BF|＜|AC|+|BD|，即|AB|＜|AC|+|BD|，
∵以AB为直径的圆半径为r=
|AB|，|MN|=（|AC|+|BD|）∴圆M到l的距离|MN|＞r，可得直线l与以AB为直径的圆相离
故选：C
点评：本题给出椭圆的右焦点F，求以经过F的弦AB为直径的圆与右准线的位置关系，着重考查了椭圆的简单几何性质、圆锥曲线的统一定义和直线与圆的位置关系等知识，属于中档题．
练习册系列答案
相关题目
+
=1（a＞b＞0）的右焦点的弦为直径的圆与其右准线的位置关系是