$\frac{tan\frac{π}{12}}{1-ta{n}^{2}\frac{π}{12}}$的值为$\frac{\sqrt{3}}{6}$．题目和参考答案——青夏教育精英家教网—

题目内容

14．$\frac{tan\frac{π}{12}}{1-ta{n}^{2}\frac{π}{12}}$的值为$\frac{\sqrt{3}}{6}$．

分析由条件利用二倍角的正切公式求得所给式子的值．

解答解：$\frac{tan\frac{π}{12}}{1-ta{n}^{2}\frac{π}{12}}$=$\frac{1}{2}$•$\frac{2tan\frac{π}{12}}{1{-tan}^{2}\frac{π}{12}}$=$\frac{1}{2}$tan$\frac{π}{6}$=$\frac{\sqrt{3}}{6}$，
故答案为：$\frac{\sqrt{3}}{6}$．

点评本题主要二倍角的正切公式的应用，属于基础题．

练习册系列答案

相关题目

4．

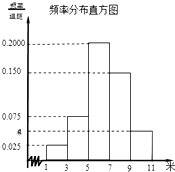为了解某校今年高一年级女生的身体素质状况，从该校高一年级女生中抽取了一部分学生进行“掷铅球”的项目测试，成绩低于5米为不合格，成绩在5至7米（含5米不含7米）的为及格，成绩在7米至11米（含7米和11米，假定该校高一女生掷铅球均不超过11米）为优秀．把获得的所有数据，分成[1，3），[3，5），[5，7），[7，9），[9，11]五组，画出的频率分布直方图如图所示．已知有4名学生的成绩在9米到11米之间．
（1）求实数a的值；
（2）参加“掷铅球”项目测试的人数．

5．设函数h（x）=$\frac{1}{2}a{x^2}$+2ax（a∈R），g（x）=lnx．
（1）若f（x）=h（x）-3g（x）在x=1处有极值，求a；
（2）若f（x）在[2，3]上为增函数，求a的取值范围；
（3）证明：?x∈（0，+∞），$\frac{x-1}{x}$≤g（x）≤x-1．

2．关于函数$f（x）={sin^2}x-{（\frac{2}{3}）^{|x|}}+\frac{1}{2}$，有下面四个结论：
①f（x）是偶函数；
②无论x取何值时，f（x）＜$\frac{1}{2}$恒成立；
③f（x）的最大值是$\frac{3}{2}$；
④f（x）的最小值是-$\frac{1}{2}$．
其中正确的结论是①④．

9．求sin（-1320°）+3cos（-420°）+3tan510°+tan（-945°）的值．

19．已知函数f（x）=sin²ωx+$\sqrt{3}$sinωxsin（ωx+$\frac{π}{2}$）（ω＞0）的最小正周期为π．
（1）求ω的值；
（2）求函数f（x）的取值范围．

6．如果sinα=$\frac{5}{13}，α∈（\frac{π}{2}，π）$，那么cosα等于（　　）

3．设函数f（x）在x=x₀处有导数，且$\underset{lim}{△x→0}$$\frac{f（{x}_{0}+2△x）-f（{x}_{0}）}{△x}$=1，则f′（x₀）=（　　）

4．经过点P（2，3），且与定圆x²+y²=4相切的直线的方程5x-12y+26=0或x=2．

试题分类