题目内容
已知以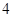 为周期的函数
为周期的函数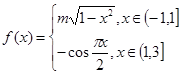 ,其中
,其中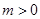 。若方程
。若方程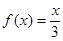 恰有5个实数解,则
恰有5个实数解,则 的取值范围为 ( )
的取值范围为 ( )
A.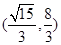 | B.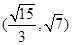 | C. | D.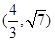 . . |
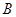
解析试题分析:∵当x∈(-1,1]时,将函数化为方程x2+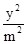 =1(y≥0),
=1(y≥0),
∴图象为半个椭圆,其图象如图所示,
同时在坐标系中作出当x∈(1,3]得图象,再根据周期性作出函数其它部分的图象,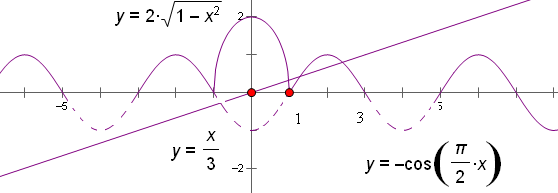
由图易知直线 y=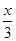 与第二个椭圆(x-4)2+
与第二个椭圆(x-4)2+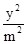 =1(y≥0)相交,而与第三个半椭圆(x-8)2+
=1(y≥0)相交,而与第三个半椭圆(x-8)2+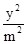 ="1" (y≥0)无公共点时,方程恰有5个实数解,
="1" (y≥0)无公共点时,方程恰有5个实数解,
将 y=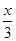 代入(x-4)2+
代入(x-4)2+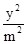 =1(y≥0)得,(9m2+1)x2-72m2x+135m2=0,令t=9m2(t>0),
=1(y≥0)得,(9m2+1)x2-72m2x+135m2=0,令t=9m2(t>0),
则(t+1)x2-8tx+15t=0,由△=(8t)2-4×15t (t+1)>0,得t>15,由9m2>15,且m>0得 m >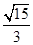 ,
,
同样将 y=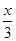 代入第三个椭圆方程(x-8)2+
代入第三个椭圆方程(x-8)2+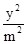 ="1" (y≥0),由△<0可计算得 m<
="1" (y≥0),由△<0可计算得 m<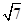 ,
,
综上可知m∈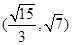 ,故选B。
,故选B。
考点:本题主要考查分段函数的概念及其图象,直线与椭圆的位置关系,函数的周期性。
点评:中档题,解的思路比较明确,首先数形结合,分析方程存在5个解时,的情况,通过建立方程组,利用判别式受到的限制进一步解题。

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
函数 的定义域是 ( )
的定义域是 ( )
| A.[-1,1] | B.(-1,1) |
| C.(1 ,+∞) | D.(-∞,2)∪(2,+∞) |
设 ,则( )
,则( )
A. | B. | C. | D. |
已知 ,则f(3)为 ( )
,则f(3)为 ( )
| A.2 | B. 3 | C. 4 | D.5 |
函数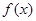 是定义在R上的奇函数,在
是定义在R上的奇函数,在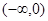 上递增,且
上递增,且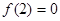 ,则使得
,则使得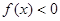 成立的
成立的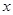 的取值范围是( )
的取值范围是( )
A.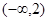 | B.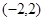 |
C. | D.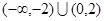 |
函数 的零点个数为( )
的零点个数为( )
| A.0 | B.1 | C.2 | D.3 |
已知函数 的两个零点分别在区间
的两个零点分别在区间 和区间
和区间 内,则实数
内,则实数 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
如果函数
 =x
=x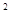 +2(a-1)x+2在区间(-∞,4)上是减函数,则实数a的取值范围是( )。
+2(a-1)x+2在区间(-∞,4)上是减函数,则实数a的取值范围是( )。
| A.a≥-3 | B. a≤-3 | C. a≤5 | D. a≥3 |
若 ,不等式
,不等式 的解集为
的解集为 ,关于
,关于 的不等式
的不等式 的解集记为
的解集记为 ,已知
,已知 是
是 的充分不必要条件,则实数
的充分不必要条件,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |