题目内容
函数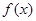 是定义在R上的奇函数,在
是定义在R上的奇函数,在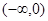 上递增,且
上递增,且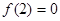 ,则使得
,则使得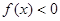 成立的
成立的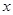 的取值范围是( )
的取值范围是( )
A.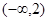 | B.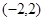 |
C. | D.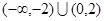 |
D
解析试题分析:根据题意,那么函数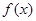 是定义在R上的奇函数,在
是定义在R上的奇函数,在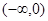 上递增,利用对称性可知在x>0时函数递增,且f(-2)=-f(2)=0,那么结合题意作图可知,满足不等式
上递增,利用对称性可知在x>0时函数递增,且f(-2)=-f(2)=0,那么结合题意作图可知,满足不等式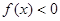 成立的x的取值范围是
成立的x的取值范围是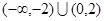 ,选D.
,选D.
考点:抽象函数的性质的运用
点评:主要是考查了抽象函数的奇偶性和单调性的运用,以及解不等式,属于中档题。

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
设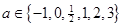 ,则使函数
,则使函数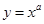 的定义域为R且为奇函数的所有
的定义域为R且为奇函数的所有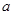 的值有( )
的值有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
设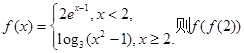 的值为 ( )
的值为 ( )
| A.0 | B.1 | C.2 | D.3 |
A,B,C是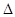 ABC的三个内角,且
ABC的三个内角,且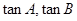 是方程
是方程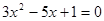 的两个实数根,则
的两个实数根,则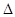 ABC是( )
ABC是( )
| A.等边三角形 | B.锐角三角形 | C.等腰三角形 | D.钝角三角形 |
若函数 在区间
在区间 上的最大值是最小值的
上的最大值是最小值的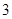 倍,则
倍,则 的值为( )
的值为( )
A. | B. | C. | D. |
已知以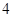 为周期的函数
为周期的函数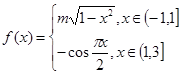 ,其中
,其中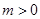 。若方程
。若方程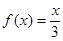 恰有5个实数解,则
恰有5个实数解,则 的取值范围为 ( )
的取值范围为 ( )
A.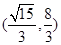 | B.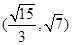 | C. | D.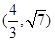 . . |
在平面直角坐标系中,横坐标、纵坐标均为整数的点称为整点,如果函数 的图象恰好通过
的图象恰好通过 个整点,则称函数
个整点,则称函数 为
为 阶整点函数。有下列函数:
阶整点函数。有下列函数: ; ②
; ② ③
③ ④
④ ,
,
其中是一阶整点函数的是( )
| A.①②③④ | B.①③④ | C.①④ | D.④ |
当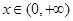 时,幂函数
时,幂函数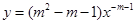 为减函数,则实数
为减函数,则实数 ( )
( )
| A.m=2 | B.m=-1 | C.m=2或m=-1 | D. |
按复利计算,存入一笔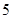 万元的三年定期存款,年利率为
万元的三年定期存款,年利率为 ,则
,则 年后支取可获得利息为( )
年后支取可获得利息为( )
A. 万元 万元 | B. 万元 万元 |
C. 万元 万元 | D. 万元 万元 |