题目内容
17.圆ρ=10$\sqrt{3}$cosθ-10sinθ的圆心极坐标是(10,-$\frac{π}{6}$).分析 把圆化为普通方程,求出圆心(5$\sqrt{3}$,-5),由$ρ=\sqrt{(5\sqrt{3})^{2}+(-5)^{2}}$=10,cosθ=$\frac{\sqrt{3}}{2}$,(5$\sqrt{3}$,-5)在第四象限,能求出圆ρ=10$\sqrt{3}$cosθ-10sinθ的圆心极坐标.
解答 解:∵圆ρ=10$\sqrt{3}$cosθ-10sinθ,
∴${ρ}^{2}=10\sqrt{3}ρcosθ-10ρsinθ$,
∴${x}^{2}+{y}^{2}=10\sqrt{3}x-10y$,
∴(x-5$\sqrt{3}$)2+(y+5)2=100,
∴圆心(5$\sqrt{3}$,-5),
∴$ρ=\sqrt{(5\sqrt{3})^{2}+(-5)^{2}}$=10,
cosθ=$\frac{5\sqrt{3}}{\sqrt{(5\sqrt{3})^{2}+(-5)^{2}}}$=$\frac{\sqrt{3}}{2}$,(5$\sqrt{3}$,-5)在第四象限,
∴$θ=-\frac{π}{6}$,
∴圆ρ=10$\sqrt{3}$cosθ-10sinθ的圆心极坐标是(10,-$\frac{π}{6}$).
故答案为:(10,-$\frac{π}{6}$).
点评 本题考查圆心的极坐标方程的求法,是基础题,解题时要认真审题,注意极坐标方程与普通方程的互化公式的合理运用.

练习册系列答案
相关题目
2.下列各式不成立的是( )
| A. | $\overrightarrow{a}$+$\overrightarrow{b}$=$\overrightarrow{b}$+$\overrightarrow{a}$ | B. | $\overrightarrow{a}$+$\overrightarrow{0}$=$\overrightarrow{a}$ | C. | $\overrightarrow{AC}$+$\overrightarrow{CB}$=$\overrightarrow{AB}$ | D. | |$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|+|$\overrightarrow{b}$| |
2.在极坐标系中,设曲线C1:ρ=2sinθ与C2:ρ=2cosθ的交点分别为A,B,则线段AB的垂直平分线的极坐标方程为( )
| A. | ρ=$\frac{1}{sinθ+cosθ}$ | B. | ρ=$\frac{1}{sinθ-cosθ}$ | C. | θ=$\frac{π}{4}$(ρ∈R) | D. | θ=$\frac{3π}{4}$(ρ∈R) |
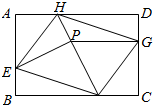 如图,矩形ABCD的边长为6和4.□EFGH的顶点在矩形的边上,并且AH=CF=2,AE=CG=3.点P在FH上,并且S四边形AEPH=5,则S四边形PFCG=8.
如图,矩形ABCD的边长为6和4.□EFGH的顶点在矩形的边上,并且AH=CF=2,AE=CG=3.点P在FH上,并且S四边形AEPH=5,则S四边形PFCG=8.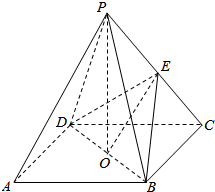 如图ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证:
如图ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证: 如图四棱柱ABCD-A1B1C1D1中,AA1⊥面ABCD,四边形ABCD为梯形,AD∥BC,且AD=3BC,过A1,C,D三点的平面记为α,BB1与α的交点为Q,则以下四个结论:
如图四棱柱ABCD-A1B1C1D1中,AA1⊥面ABCD,四边形ABCD为梯形,AD∥BC,且AD=3BC,过A1,C,D三点的平面记为α,BB1与α的交点为Q,则以下四个结论: