题目内容
12.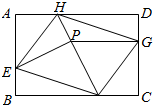 如图,矩形ABCD的边长为6和4.□EFGH的顶点在矩形的边上,并且AH=CF=2,AE=CG=3.点P在FH上,并且S四边形AEPH=5,则S四边形PFCG=8.
如图,矩形ABCD的边长为6和4.□EFGH的顶点在矩形的边上,并且AH=CF=2,AE=CG=3.点P在FH上,并且S四边形AEPH=5,则S四边形PFCG=8.
分析 先求出S△AEH=S△CGF=3,从而S△PEH=S四边形AEPH-S△AEH=5-3=2,再由S△PEH+S△GPF=$\frac{1}{2}{S}_{?EFGH}$=$\frac{1}{2}$[S矩形ABCD-(S△AEH+S△BEF+S△CGF+S△GDH)],求出S△GPF,由此能求出S四边形PFCG.
解答 解:∵矩形ABCD的边长为6和4.?EFGH的顶点在矩形的边上,
且AH=CF=2,AE=CG=3.点P在FH上,并且S四边形AEPH=5,
∴S△AEH=S△CGF=$\frac{1}{2}×2×3=3$,∴S△PEH=S四边形AEPH-S△AEH=5-3=2,
∵S△PEH+S△GPF=$\frac{1}{2}{S}_{?EFGH}$=$\frac{1}{2}$[S矩形ABCD-(S△AEH+S△BEF+S△CGF+S△GDH)]
=$\frac{1}{2}$[6×4-$\frac{1}{2}$(2×3+1×4+2×3+1×4)]
=7,
∴S△GPF=7-SPEH=7-2=5.
∴S四边形PFCG=S△GPF+S△CGF=5+3=8.
故答案为:8.
点评 本题考查四边形面积的求法,是中档题,解题时要认真审题,注意平面图形面积公式的合理运用.

练习册系列答案
相关题目
15.若2cos($\frac{π}{2}$-α)-sin($\frac{3}{2}$π+α)=-$\sqrt{5}$,则tanα=( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
 已知在四棱锥S-ABCD中,四边形ABCD是菱形,SD⊥平面ABCD,P为SB的中点,Q为BD上一动点.AD=2,SD=2,∠DAB=$\frac{π}{3}$.
已知在四棱锥S-ABCD中,四边形ABCD是菱形,SD⊥平面ABCD,P为SB的中点,Q为BD上一动点.AD=2,SD=2,∠DAB=$\frac{π}{3}$.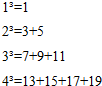 已知任意一个正整数的三次幂均可表示成一些连续奇数的和,如图所示,33可以表示为7+9+11,我们把7,9,11叫做33的“质数因子”,若n3的一个“质数因子”为2013,则n为( )
已知任意一个正整数的三次幂均可表示成一些连续奇数的和,如图所示,33可以表示为7+9+11,我们把7,9,11叫做33的“质数因子”,若n3的一个“质数因子”为2013,则n为( )