题目内容
在△ABC中,如果sinA=cosB,那么这个三角形是( )
| A.直角三角形 |
| B.锐角三角形 |
| C.钝角三角形 |
| D.直角三角形或钝角三角形 |
∵sinA=cosB>0,B是三角形内角,∴B为锐角.
又∵cosB=sin(90°-B),sinA=cosB,
∴sinA=sin(90°-B),
∴①∠A=90°-∠B,
∴∠A+∠B=90°,
∴∠C=90°.即三角形是直角三角形.
②∠A=180°-90°+∠B,
∴∠A=90°+∠B,A为钝角,三角形是钝角三角形.
故选:D.
又∵cosB=sin(90°-B),sinA=cosB,
∴sinA=sin(90°-B),
∴①∠A=90°-∠B,
∴∠A+∠B=90°,
∴∠C=90°.即三角形是直角三角形.
②∠A=180°-90°+∠B,
∴∠A=90°+∠B,A为钝角,三角形是钝角三角形.
故选:D.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 ,
, 时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.⑴试确定A,
时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.⑴试确定A, 和
和 的值;⑵现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设
的值;⑵现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设 (弧度),试用
(弧度),试用 来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)
来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)
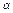 是锐角,
是锐角,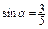 ,则
,则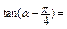
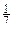

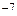
 的模为
的模为 ,则
,则 等于
等于