题目内容

△ABC中，若sinA=2sinBcosC，sin2A=sin2B+sin2C，试判断△ABC的形状．
已知等式sinA=2sinBcosC，变形得：sin（B+C）=sinBcosC+cosBsinC=2sinBcosC，
整理得：sinBcosC-cosBsinC=sin（B-C）=0，
∵B与C都为三角形内角，∴B-C=0，即B=C，
利用正弦定理化简sin2A=sin2B+sin2C，得：a2=b2+c2，
则△ABC为等腰直角三角形．
练习册系列答案
相关题目
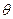为第二象限的角，则必有 （   ）
A．＞B．＜
C．＞D．＜
直线l的倾斜角为θ，sinθ+cosθ=
7
13
，则斜率k的值为（　　）
A．-
12
5
B．
12
5
C．-
12
5
或-
5
12
D．-
5
12
在△ABC中，如果sinA=cosB，那么这个三角形是（　　）
A．直角三角形
B．锐角三角形
C．钝角三角形
D．直角三角形或钝角三角形
在△ABC中，a=λ，b=
3
λ（λ＞0），∠A=45°则满足此条件的三角形有（　　）
A．0个B．1个C．2个D．无数个
在△ABC中，acosA=bcosB，则三角形的形状为（　　）
A．直角三角形
B．等腰三角形或直角三角形
C．等边三角形
D．等腰三角形
已知△ABC满足c=2acosB，则△ABC的形状是（　　）
A．等腰三角形
B．直角三角形
C．等腰直角三角形
D．等腰三角形或直角三角形
若不等式a＞2sinxcosx+
3
cos2x恒成立，则实数a的取值范围为______．
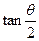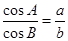在△ABC中，已知，则△ABC的形状为          .

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网