题目内容
已知tan2α=
,α∈(0,
),则
=______.
| 3 |
| 4 |
| π |
| 4 |
| sinα+cosα |
| sinα-cosα |
tan2α=
=
,
整理得:3tan2α+8tanα-3=0,即(3tanα-1)(tanα+3)=0,
解得:tanα=
或tanα=-3,
∵α∈(0,
),
∴tanα=
,
则原式=
=
=-2.
故答案为:-2
| 2tanα |
| 1-tan2α |
| 3 |
| 4 |
整理得:3tan2α+8tanα-3=0,即(3tanα-1)(tanα+3)=0,
解得:tanα=
| 1 |
| 3 |
∵α∈(0,
| π |
| 4 |
∴tanα=
| 1 |
| 3 |
则原式=
| tanα+1 |
| tanα-1 |
| ||
|
故答案为:-2

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 有最大值
有最大值 和最小值
和最小值 ,求实数
,求实数 的值。
的值。 ,
, ,则
,则 ______
______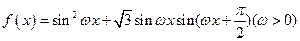 的最小正周期为
的最小正周期为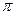 ,
,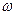 的值;(2)求函数
的值;(2)求函数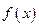 在区间
在区间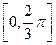 上的取值范围.
上的取值范围.