题目内容
【题目】已知椭圆 C:![]() 的焦距为2,且过点
的焦距为2,且过点![]() ,右焦点为
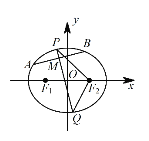
,右焦点为![]() .设A,B 是C上的两个动点,线段 AB 的中点M 的横坐标为
.设A,B 是C上的两个动点,线段 AB 的中点M 的横坐标为![]() ,线段AB的中垂线交椭圆C于P,Q 两点.
,线段AB的中垂线交椭圆C于P,Q 两点.
(1)求椭圆 C 的方程;
(2)设M点纵坐标为m,求直线PQ的方程,并求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用椭圆C:![]() (a>b>0)的焦距为2,且过点(1,
(a>b>0)的焦距为2,且过点(1,![]() ),建立方程组,求出a,b,即可求椭圆C的方程;
),建立方程组,求出a,b,即可求椭圆C的方程;
(2)分类讨论,求出直线PQ的方程,与椭圆方程联立,结合向量的数量积,![]() 在椭圆的内部,利用换元法,即可求
在椭圆的内部,利用换元法,即可求![]() 的取值范围.
的取值范围.
(1) 因为椭圆 ![]() 的焦距为
的焦距为 ![]() ,且过点K
,且过点K ![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,于是
,于是 ![]() ,
,![]() ,所以椭圆
,所以椭圆 ![]() 的方程为
的方程为 ![]() .
.
(2) 由题意,当直线 ![]() 垂直于
垂直于 ![]() 轴时,直线
轴时,直线 ![]() 方程为
方程为 ![]() ,此时
,此时 ![]() ,
,![]() ,得
,得 ![]() .
.
当直线 ![]() 不垂直于
不垂直于 ![]() 轴时,设直线
轴时,设直线 ![]() 的斜率为
的斜率为 ![]() ,
,![]() ,
,![]() ,
,![]() ,由线段
,由线段 ![]() 的中点
的中点 ![]() 的横坐标为
的横坐标为 ![]() ,得
,得 ![]() ,则
,则 ![]() ,故
,故 ![]() .此时,直线
.此时,直线 ![]() 斜率为
斜率为 ![]() ,
,![]() 的直线方程为
的直线方程为 ![]() ,即
,即 ![]() .联立
.联立 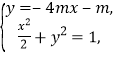 消去
消去 ![]() ,整理得
,整理得 ![]() .设
.设 ![]() ,
,![]() ,所以
,所以 ![]() ,
,![]() ,
,
于是 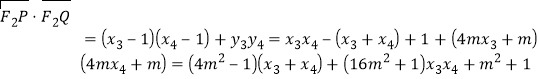
![]()
![]()
由于 ![]() 在椭圆的内部,故
在椭圆的内部,故 ![]() ,令
,令 ![]() ,
,![]() ,
,
则 ![]() .又
.又 ![]() ,所以
,所以 ![]() .综上,
.综上,![]() 的取值范围为
的取值范围为 ![]() .
.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目