题目内容
已知函数y=ax(a>0,且a≠1)和y=lg(ax2-x+a).则p:关于x的不等式ax>1的解集是(-∞,0);q:函数y=lg(ax2-x+a)的定义域为R.如果p和q有且只有一个正确,求a的取值范围.
【答案】分析:根据所给的两个命题看出P命题是一个真命题时对应的a的值,Q命题是一个真命题时对应的a的值,P与Q中有且仅有一个正确,对两个命题的真假进行讨论,得到a的取值范围.
解答:解:∵P:关于x的不等式ax>1的解集是(-∞,0),
∴0<a<1; (1分)
又Q真?ax2-x+a>0对?x∈R恒成立?△=1-4a2<0?- <a<
<a< .(3分)
.(3分)
P真Q假?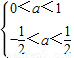 ?0<a<
?0<a< (5分)
(5分)
P假Q真?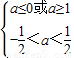 ?-
?- <a≤0(7分)
<a≤0(7分)
综上有实数a的取值范围是(- ,
, )(8分)
)(8分)
点评:本题看出命题真假的判断和二次函数的性质,本题解题的关键是对于两个命题一真一假的字母的取值的判断,本题是一个综合题目.
解答:解:∵P:关于x的不等式ax>1的解集是(-∞,0),
∴0<a<1; (1分)
又Q真?ax2-x+a>0对?x∈R恒成立?△=1-4a2<0?-
 <a<
<a< .(3分)
.(3分)P真Q假?
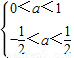 ?0<a<
?0<a< (5分)
(5分)P假Q真?
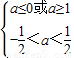 ?-
?- <a≤0(7分)
<a≤0(7分)综上有实数a的取值范围是(-
 ,
, )(8分)
)(8分)点评:本题看出命题真假的判断和二次函数的性质,本题解题的关键是对于两个命题一真一假的字母的取值的判断,本题是一个综合题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数y=ax(a>1)在区间[1,2]上的最大值与最小值之差为2,则实数a的值为( )
A、
| ||
| B、2 | ||
| C、3 | ||
| D、4 |