题目内容
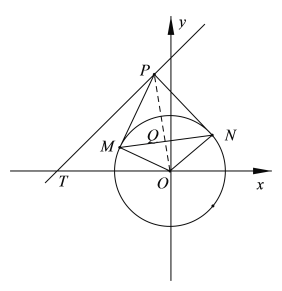
【题目】在平面直角坐标系xOy中,已知直线l:x﹣y+4=0和圆O:x2+y2=4,P是直线l上一点,过点P作圆C的两条切线,切点分别为M,N.
(1)若PM⊥PN,求点P坐标;
(2)若圆O上存在点A,B,使得∠APB=60°,求点P的横坐标的取值范围;
(3)设线段MN的中点为Q,l与x轴的交点为T,求线段TQ长的最大值.
【答案】(1)P(﹣2,2);(2)[﹣4,0];(3)3![]()
【解析】
(1)由PM⊥PN,则四边形PMON为正方形,可得![]() 到圆心距离,由此可求得
到圆心距离,由此可求得![]() 点坐标;
点坐标;
(2)设P(x,x+4),过P作圆的切线PC,PD,若圆O上存在点A,B,使得∠APB=60°,则∠CPD≥600,把它用坐标![]() 表示后可得
表示后可得![]() 范围;
范围;
(3)设P(x0,x0+4),得以OP为直径的圆的方程与x2+y2=4联立(相减)可得MN所在直线方程,由直线![]() 方程与x2+y2=4联立消元后用韦达定理可求得
方程与x2+y2=4联立消元后用韦达定理可求得![]() 点的横坐标,再得纵坐标,消去参数后得
点的横坐标,再得纵坐标,消去参数后得![]() 点轨迹方程,轨迹是圆(去掉原点),求出
点轨迹方程,轨迹是圆(去掉原点),求出![]() 点坐标后,由点与圆的位置关系可得最大值.
点坐标后,由点与圆的位置关系可得最大值.
(1)若PM⊥PN,则四边形PMON为正方形,则P到圆心的距离为![]() ,∵P在直线x﹣y+4=0上,设P(x,x+4)
,∵P在直线x﹣y+4=0上,设P(x,x+4)
故|OP|![]() ,解得x=﹣2,故P(﹣2,2);
,解得x=﹣2,故P(﹣2,2);
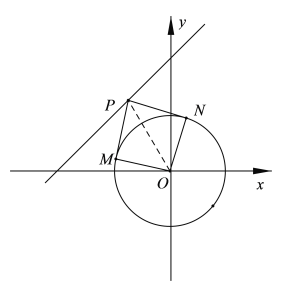
(2)设P(x,x+4),若圆O上存在点A,B,使得∠APB=60°,过P作圆的切线PC,PD,∴∠CPD≥600,∴∠CPO≥300,
在直角三角形△CPO中,∵300≤∠CPO<900,
∴![]() sin∠CPO<1,即
sin∠CPO<1,即![]() 1,∴2
1,∴2![]() OP≤4,
OP≤4,
∴2![]() 4,解得﹣4≤x≤0,∴点P的横坐标的取值范围为:[﹣4,0];
4,解得﹣4≤x≤0,∴点P的横坐标的取值范围为:[﹣4,0];
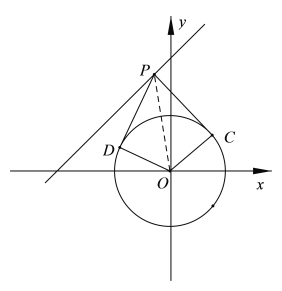
(3)设P(x0,x0+4),则以OP为直径的圆的方程为![]() ,
,
化简得![]() ,与x2+y2=4联立,可得MN所在直线方程:x0x+(x0+4)y=4,
,与x2+y2=4联立,可得MN所在直线方程:x0x+(x0+4)y=4,
联立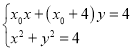 ,得
,得![]() ,
,
![]() ,∴
,∴![]() ,所以
,所以![]() ,
,
∴Q的坐标为(![]() ,
,![]() ),
),
由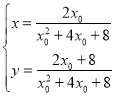 ,得
,得![]() ,
,![]() ,代入化简可得Q点的轨迹方程为:
,代入化简可得Q点的轨迹方程为:![]() ,圆心C(
,圆心C(![]() ,
,![]() ),半径R
),半径R![]() .
.
其中原点(0,0)为极限点(也可以去掉).由题可知T(﹣4,0),
∴|TC|![]() .∴|TQ|≤|TC|+R=3
.∴|TQ|≤|TC|+R=3![]() .∴线段TQ长的最大值为3
.∴线段TQ长的最大值为3![]() .
.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人,第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:

(1)根据茎叶图判断哪种生产方式的效率更高?并说明理由;
(2)求40名工人完成生产任务所需时间的中位数![]() ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的工人数填入下面的列联表:
的工人数填入下面的列联表:
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
(3)根据(2)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:![]() ,
,
|
|
|
|
|
|
|
|