题目内容
【题目】设a,b∈R.若直线l:ax+y﹣7=0在矩阵A= ![]() 对应的变换作用下,得到的直线为l′:9x+y﹣91=0.求实数a,b的值.
对应的变换作用下,得到的直线为l′:9x+y﹣91=0.求实数a,b的值.
【答案】解:方法一:在直线l:ax+y﹣7=0取A(0,7),B(1,7﹣a), 由 ![]()
![]() =
= ![]() ,则
,则 ![]()
![]() =
=  ,
,
则A(0,7),B(1,7﹣a)在矩阵A对应的变换作用下A′(0,7b),B′(3,b(7﹣a)﹣1),
由题意可知:A′,B′在直线9x+y﹣91=0上,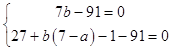 ,解得:
,解得: ![]() ,
,
实数a,b的值2,13.
方法二:设直线l上任意一点P(x,y),点P在矩阵A对应的变换作用下得到Q(x′,y′),
则 ![]()
![]() =
= ![]() ,
,
∴ ![]() ,
,
由Q(x′,y′),在直线l′:9x+y﹣91=0.即27x+(﹣x+by)﹣91=0,
即26x+by﹣91=0,
P在ax+y﹣7=0,则ax+y﹣7=0,
∴ ![]() =
= ![]() =
= ![]() ,
,
解得:a=2,b=13.
实数a,b的值2,13
【解析】方法一:任取两点,根据矩阵坐标变换,求得A′,B′,代入直线的直线为l′即可求得a和b的值;方法二:设P(x,y),利用矩阵坐标变换,求得Q点坐标,代入直线为l′,由ax+y﹣7=0,则 ![]() =
= ![]() =
= ![]() ,即可求得a和b的值.
,即可求得a和b的值.

练习册系列答案
相关题目