题目内容
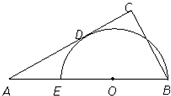（几何证明选讲）如图，已知EB是半圆O的直径，A是BE延长线上一点，AC是半圆O的切线BC⊥AC于C，若BC=6，AC=8，则AE=分析：连接OD证得OD∥BC，由此得比例关系
=
，再由题设条件求得AB=10，OD，AO用要求的量AE表示出来，代入比例式即可得到AE的方程，求解既得．
| OD |
| BC |
| AO |
| AB |
解答：解：连接OD，由于AD是半圆O的切线，故角ADO=90°，又BC⊥AC于C可得OD∥BC
∵BC=6，AC=8，∴AB=10，∴AE+2R=10，∴R=5-
由OD∥BC得
=
，即
=
解得AE=
故答案为
∵BC=6，AC=8，∴AB=10，∴AE+2R=10，∴R=5-
| AE |
| 2 |
由OD∥BC得
| OD |
| BC |
| AO |
| AB |
5-
| ||
| 6 |
5+
| ||
| 10 |
| 5 |
| 2 |
故答案为
| 5 |
| 2 |
点评：本题考查直线与圆的位置关系，及圆内的有关的比例线段，求解本题的关键是由平行关系得到比例式及用要求的量AE将比例式中的各个量表示出来．
练习册系列答案
阅读快车系列答案
相关题目
（选修4-1：几何证明选讲）
（几何证明选讲）如图，AB、CD是圆O的两条弦，且AB是线段CD的中垂线，已知AB=10，CD=8，则线段AC的长度为
（1）几何证明选讲：如图，CB是⊙O的直径，AP是⊙O的切线，A为切点，AP与CB的延长线交于点P，若PA=8，PB=4，求AC的长度．
选修4-1：几何证明选讲．
（1）（几何证明选讲）如图，AB是半圆O的直径，点C在半圆上，CD⊥AB，垂足为D，且AD=5DB，设∠COD=θ，则tanθ的值为