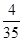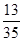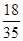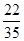题目内容
某中学在高三开设了4门选修课,每个学生必须且只需选修1门选修课。对于该年级的甲、乙、丙3名学生,回答下面的问题:
(1)求这3名学生选择的选修课互不相同的概率;
(2)某一选修课被这3名学生选修的人数的数学期望.
(1)求这3名学生选择的选修课互不相同的概率;
(2)某一选修课被这3名学生选修的人数的数学期望.
解:(1) 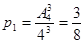 ;
;
(2)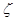 的分布列为
的分布列为
数学期望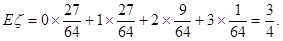
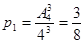 ;
;(2)
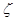 的分布列为
的分布列为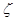 | 0 | 1 | 2 | 3 |
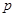 | 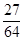 | 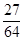 | 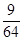 |  |
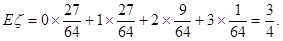
此题主要考查离散型随机变量的期望和方差,此类题也是高考必考的热点,平时我们要多加练习.
(I)已知高二开设了4门选修课,每个学生必须且只需选修1门选修课,每一人都有4种选择,总共有43,互不相同的则有A43,从而求解;
(II)某一选修课被这3名学生选择的人数为ξ,则ξ=0,1,2,3,分别算出P(ξ=0),P(ξ=1),P(ξ=2),P(ξ=3),P(ξ=4),再利用期望公式求解
(I)已知高二开设了4门选修课,每个学生必须且只需选修1门选修课,每一人都有4种选择,总共有43,互不相同的则有A43,从而求解;
(II)某一选修课被这3名学生选择的人数为ξ,则ξ=0,1,2,3,分别算出P(ξ=0),P(ξ=1),P(ξ=2),P(ξ=3),P(ξ=4),再利用期望公式求解

练习册系列答案
相关题目
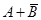 发生的概率为___________________
发生的概率为___________________
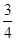
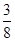
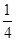
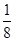
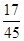
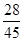
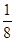
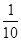
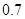 (假定每次通过率相同).
(假定每次通过率相同).