题目内容
(2013•盐城二模)设函数fn(x)=-xn+3ax+b(n∈N*,a,b∈R).
(1)若a=b=1,求f3(x)在[0,2]上的最大值和最小值;
(2)若对任意x1,x2∈[-1,1],都有|f3(x1)-f3(x2)|≤1,求a的取值范围;
(3)若|f4(x)|在[-1,1]上的最大值为
,求a,b的值.
(1)若a=b=1,求f3(x)在[0,2]上的最大值和最小值;
(2)若对任意x1,x2∈[-1,1],都有|f3(x1)-f3(x2)|≤1,求a的取值范围;
(3)若|f4(x)|在[-1,1]上的最大值为
| 1 | 2 |
分析:(1)把a,b的值代入函数解析式求出f3(x)=-x3+3x+1,求导后利用导函数的零点将(0,2)分段,由单调性判出极值点,求出极值,再求出端点值,则f3(x)在[0,2]上的最大值和最小值可求;
(2)根据对任意x1,x2∈[-1,1],都有|f3(x1)-f3(x2)|≤1,说明当x取两个特殊值-1和1时|f3(1)-f3(-1)|≤1成立,由此求出a的初步范围,然后把原函数f3(x)求导,得到导函数的两个零点为-
,
,再求出函数f3(x)在(-1,1)上的极大值和极小值,再由极大值和极小值差的绝对值小于等于1求出a的取值范围,和由|f3(1)-f3(-1)|≤1求出的a的范围取交集即可;
(3)由|f4(x)|在[-1,1]上的最大值为
,则x取-1和1时的函数值都在-
和
之间,联立解出b的范围,再由x取0时的函数值也在-
和
之间,得到b的范围,两者结合即可求出b的值,把b的值代入x取-1和1时的式子,即可得到a的值.
(2)根据对任意x1,x2∈[-1,1],都有|f3(x1)-f3(x2)|≤1,说明当x取两个特殊值-1和1时|f3(1)-f3(-1)|≤1成立,由此求出a的初步范围,然后把原函数f3(x)求导,得到导函数的两个零点为-
| a |
| a |
(3)由|f4(x)|在[-1,1]上的最大值为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)由fn(x)=-xn+3ax+b,所以当a=b=1时,f3(x)=-x3+3x+1
则
(x)=-3x2+3=-3(x2-1).
在(0,1)内,
(x)>0,在(1,2)内,
(x)<0,
所以在(0,1)内,f3(x)=-x3+3x+1为增函数,在(1,2)内f3(x)=-x3+3x+1为减函数.
则f3(x)的极大值为f3(1)=3,由f3(0)=1,f3(2)=-23+3×2+1=-1.
所以函数f3(x)=-x3+3x+1在[0,2]上的最大值为f3(1)=3,最小值为f3(2)=-1;
(2)因为对任意x1,x2∈[-1,1],都有|f3(x1)-f3(x2)|≤1,
所以|f3(1)-f3(-1)|≤1,从而有|(-1+3a+b)-(1-3a+b)|=|6a-2|≤1,
所以
≤a≤
.
又
(x)=-3x2+3a=-3(x2-a),
在[-1,-
],[
,1]内f′3(x)<0,
所以f3(x)在[-1,-
],[
,1]内为减函数,
f3(x)在[-
,
]内为增函数,
只需|f3(
)-f3(-
)|≤1,则|(-(
)3+3a
+b)-((
)3-3a
+b)|≤1
即4a
≤1,解得:a≤
.
所以a的取值范围是
≤a≤
.
(3)f4(x)=-x4+3ax+b.
由f4(x)在[-1,1]上的最大值为
,则|f4(x)|≤
,
所以-
≤f4(1)≤
,即-
≤-1+3a+b≤
①
-
≤f4(-1)≤
,即-
≤-1-3a+b≤
②
①+②得,
≤b≤
,又因为-
≤f4(0)≤
,所以-
≤b≤
,所以b=
.
将b=
代入①得:0≤a≤
,
将b=
代入②得:-
≤a≤0.
所以a=0.
综上知a,b的值分别为0,
.
则
| f | ′ 3 |
在(0,1)内,
| f | ′ 3 |
| f | ′ 3 |
所以在(0,1)内,f3(x)=-x3+3x+1为增函数,在(1,2)内f3(x)=-x3+3x+1为减函数.
则f3(x)的极大值为f3(1)=3,由f3(0)=1,f3(2)=-23+3×2+1=-1.
所以函数f3(x)=-x3+3x+1在[0,2]上的最大值为f3(1)=3,最小值为f3(2)=-1;
(2)因为对任意x1,x2∈[-1,1],都有|f3(x1)-f3(x2)|≤1,
所以|f3(1)-f3(-1)|≤1,从而有|(-1+3a+b)-(1-3a+b)|=|6a-2|≤1,
所以
| 1 |
| 6 |
| 1 |
| 2 |
又
| f | ′ 3 |
在[-1,-
| a |
| a |
所以f3(x)在[-1,-
| a |
| a |
f3(x)在[-
| a |
| a |
只需|f3(
| a |
| a |
| a |
| a |
| a |
| a |
即4a
| a |
| 1 | |||
|
所以a的取值范围是
| 1 |
| 6 |
| 1 | |||
|
(3)f4(x)=-x4+3ax+b.
由f4(x)在[-1,1]上的最大值为
| 1 |
| 2 |
| 1 |
| 2 |
所以-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
①+②得,
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
将b=
| 1 |
| 2 |
| 1 |
| 3 |
将b=
| 1 |
| 2 |
| 1 |
| 6 |
所以a=0.
综上知a,b的值分别为0,
| 1 |
| 2 |
点评:本题考查了利用导数研究函数的最值,考查了数学转化思想方法,解答此题的关键是特值化思想的应用,求具体参数的值时运用了“两边夹”的思想方法,属有一定难度题.

练习册系列答案
相关题目
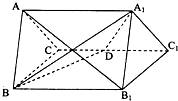 (2013•盐城二模)正三棱柱ABC-A1B1C1的所有棱长都为4,D为的CC1中点.
(2013•盐城二模)正三棱柱ABC-A1B1C1的所有棱长都为4,D为的CC1中点.