题目内容
(2013•盐城二模)设函数y=f(x)满足对任意的x∈R,f(x)≥0且f2(x+1)+f2(x)=9.已知当x∈[0,1]时,有f(x)=2-|4x-2|,则f(
)的值为
.
| 2013 |
| 6 |
| 5 |
| 5 |
分析:由条件求得可得 f(x+2)=f(x),故函数是周期为2的周期函数,可得 f(
)=f(-
),先求得f(
)的值,
根据f2(x+1)+f2(x)=9,即可求得f(-
)的值,从而求得 f(
) 的值.
| 2013 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
根据f2(x+1)+f2(x)=9,即可求得f(-
| 1 |
| 2 |
| 2013 |
| 6 |
解答:解:∵f2(x+1)+f2(x)=9,即 f2(x+1)=9-f2(x),
∴f2(x+2)=9-f2(x+1),化简可得 f2(x+2)=9-[9-f2(x)]=f2(x).
再由 函数y=f(x)满足对任意的x∈R,f(x)≥0,可得 f(x+2)=f(x),故函数是周期为2的周期函数.
∴f(
)=f(336-
)=f(-
).
又 f2(-
)=9-f2(-
+1)=9-f2(
),
再由当x∈[0,1]时,有f(x)=2-|4x-2|,可得f(
)=2-|4×
-2|=2,
故 f2(-
)=9-f2(
)=9-4=5,故f(-
)=
,
故f(
)=f(-
)=
,
故答案为
.
∴f2(x+2)=9-f2(x+1),化简可得 f2(x+2)=9-[9-f2(x)]=f2(x).
再由 函数y=f(x)满足对任意的x∈R,f(x)≥0,可得 f(x+2)=f(x),故函数是周期为2的周期函数.
∴f(
| 2013 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
又 f2(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
再由当x∈[0,1]时,有f(x)=2-|4x-2|,可得f(
| 1 |
| 2 |
| 1 |
| 2 |
故 f2(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
故f(
| 2013 |
| 6 |
| 1 |
| 2 |
| 5 |
故答案为
| 5 |
点评:本题主要考查了抽象函数的求值,同时考查了函数的周期性,属于中档题.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
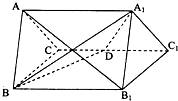 (2013•盐城二模)正三棱柱ABC-A1B1C1的所有棱长都为4,D为的CC1中点.
(2013•盐城二模)正三棱柱ABC-A1B1C1的所有棱长都为4,D为的CC1中点.