题目内容
(2013•广州二模)记实数x1,x2,…,xn中的最大数为max{x1,x2,…,xn},最小数为min{x1,x2,…,xn}则max{min{x+1,x2-x+1,-x+6}}=( )
分析:在同一坐标系中作出三个函数y=x+1,y=x2-x+1与y=-x+6的图象,依题意,即可求得max{min{x+1,x2-x+1,-x+6}}.
解答:解:在同一坐标系中作出三个函数y=x+1,y=x2-x+1与y=-x+6的图象如图: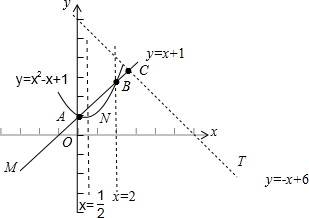
由图可知,min{x+1,x2-x+1,-x+6}为射线AM,抛物线
,线段BC,与射线CT的组合体,
显然,在C点时,y=min{x+1,x2-x+1,-x+6}取得最大值.
解方程组
得,C(
,
),
∴max{min{x+1,x2-x+1,-x+6}}=
.
故答案为
.
故选D
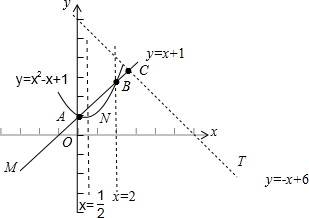
由图可知,min{x+1,x2-x+1,-x+6}为射线AM,抛物线
 |
| ANB |
显然,在C点时,y=min{x+1,x2-x+1,-x+6}取得最大值.
解方程组
|
| 5 |
| 2 |
| 7 |
| 2 |
∴max{min{x+1,x2-x+1,-x+6}}=
| 7 |
| 2 |
故答案为
| 7 |
| 2 |
故选D
点评:本题考查函数的最值及其几何意义,在同一坐标系中作出三个函数y=x+1,y=x2-x+1与y=-x+6的图象是关键,也是难点,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目