题目内容

如图，正三棱柱的九条棱都相等，三个侧面都是正方体，M、N分别是BC和A1C1的中点，求MN与CC1所成角的余弦值．
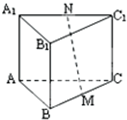
设正三棱柱的棱长为a，取AC中点O，连接MO，NO，则NO垂直平面ABC

∴∠MNO为MN与CC1所成的角
在Rt△MNO中，∠NOM=90°，NO=A1A=2a
∵M，O分别为BC，AC的中点，∴MO=
1
2
AB=a
∴MN=
NO2+MO2
=
5
a
∴cos∠MNO=
NO
MN
=
2
5
5
练习册系列答案
相关题目
已知正方体ABCD-A1B1C1D1，O是底ABCD对角线的交点．
（1）求证：C1O∥面AB1D1；
（2）求异面直线AD1与C1O所成角的大小．
长方体ABCD-A1B1C1D1中，BB1=BC，P为C1D1上一点，则异面直线PB与B1C所成角的大小（　　）
A．是45°B．是60°
C．是90°D．随P点的移动而变化
正方体ABCD-A1B1C1D1中直线A1D与平面AB1C1D所成角为（　　）
A．30°B．45°C．60°D．90°
如图，已知斜三棱柱（侧棱不垂直于底面）ABC-A1B1C1的侧面A1ACC1与底面ABC垂直，BC=2，AC=2
3
，AB=2
2
，AA1=A1C=
6
．
（Ⅰ）设AC的中点为D，证明A1D⊥底面ABC；
（Ⅱ）求异面直线A1C与AB成角的余弦值．
如图，在正方体ABCD-A1B1C1D1中，M，N分别是棱B1C1，AD的中点，则直线MN与底面ABCD所成角的大小是______．
正方体ABCD-A1B1C1D1的棱长为2，M，N分别为AA1、BB1的中点．
求：（1）CM与D1N所成角的余弦值．
（2）D1N与平面MBC所成角的余弦值．
已知二面角α-l-β等于90°，A、B是棱l上两点，AC、BD分别在半平面α、β内，AC⊥l，BD⊥l，已知AB=5，AC=3，BD=4，则CD与平面α所成角的正弦值为______．
如图：在直三棱柱ABC-DEF中，AB=2，AC=AD=2
3
，AB⊥AC，
（1）证明：AB⊥DC，
（2）求二面角A-DC-B的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网