题目内容

已知椭圆
x2
a2
+
y2
b2
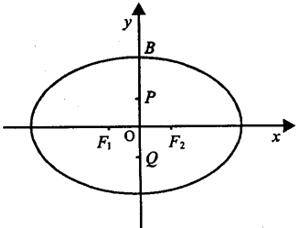
=1上到点A（0，b）距离最远的点是B（0，-b），则椭圆的离心率的取值范围为（　　）
A．(0，
6
3
]		B．[
6
3
，1)		C．(0，
2
2
]		D．[
2
2
，1)
设点P（x，y）是椭圆上的任意一点，
则
x2
a2
+
y2
b2
=1，化为x2=a2(1-
y2
b2
)．
∴|PA|2=x2+（y-b）2=a2(1-
y2
b2
)+(y-b)2=-
c2
b2
(y-
-b3
c2
)2+
a4
c2
=f（y），
∵椭圆上的点P到点A（0，b）距离最远的点是B（0，-b），
由二次函数的单调性可知：f（y）在（-b，b）单调递减，
∴
-b3
c2
≤-b，
化为c2≤b2=a2-c2，即2c2≤a2，
∴e≤
2
2
．
又e＞0．
∴离心率的取值范围是(0，
2
2
]．
故选：C．
练习册系列答案
相关题目
设P为椭圆
x2
16
+
y2
9
=1上的一点，F1、F2是椭圆的焦点，若|PF1|：|PF2|=3：1，则∠F1PF2的大小为（　　）
A．30°B．60°C．90°D．120°
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0），A（2，0）为长轴的一个端点，弦BC过椭圆的中心O，且
AC
•
BC
=0，|
OC
-
OB
|=2|
BC
-
BA
|，则其焦距为（　　）
A．
2
6
3
B．
4
3
3
C．
4
6
3
D．
2
3
3
椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率是
1
2
，则
b2+1
3a
的最小值为（　　）
A．
3
3
B．1C．
2
3
3
D．2
设椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的两个焦点是F1和F2，长轴是A1A2，P是椭圆上异于A1、A2的点，考虑如下四个命题：
①|PF1|-|A1F1|=|A1F2|-|PF2|；
②a-c＜|PF1|＜a+c；
③若b越接近于a，则离心率越接近于1；
④直线PA1与PA2的斜率之积等于-
b2
a2
．
其中正确的命题是（　　）
A．①②④B．①②③C．②③④D．①④
椭圆的长轴为A1A2，B为短轴一端点，若∠A1BA2=120°，则椭圆的离心率为（　　）
A．
6
3
B．
3
3
C．
3
2
D．
1
2
已知椭圆
x2
2
+
y2
3
=1，F1、F2是它的焦点，AB是过F1的弦，则△ABF2的周长为______．
设椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的左，右两个焦点分别为F1，F2，短轴的上端点为B，短轴上的两个三等分点为P，Q，且F1PF2Q为正方形．
（1）求椭圆的离心率；
（2）若过点B作此正方形的外接圆的切线在x轴上的一个截距为-
3
2
4
，求此椭圆方程．
椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率为
3
2
，且过点（2，0）．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设直线l：y=x+m与椭圆C交于两点A，B，O为坐标原点，若△OAB为直角三角形，求m的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网