题目内容
设函数f(x)=sin(2x+ ),则下列结论正确的是
),则下列结论正确的是
①f(x)的图象关于直线x= 对称 ②f(x)的图象关于点(
对称 ②f(x)的图象关于点( ,0)对称
,0)对称
③把f(x)的图象向左平移 个单位,得到一个偶函数的图象
个单位,得到一个偶函数的图象
④f(x)在[0, ]上为增函数
]上为增函数
- A.①②
- B.③④
- C.②③
- D.①④
C
分析:将x= 代入函数f(x)中得到f(
代入函数f(x)中得到f( )=sinπ=0,得到(
)=sinπ=0,得到( )是其对称中心,判断出①错;②对;根据函数图象平移的规律及偶函数的定义判断出③对;根据整体角处理的方法判断出④错.
)是其对称中心,判断出①错;②对;根据函数图象平移的规律及偶函数的定义判断出③对;根据整体角处理的方法判断出④错.
解答:对于①②,因为f( )=sinπ=0,所以(
)=sinπ=0,所以( )是其对称中心,故①错;②对;
)是其对称中心,故①错;②对;
对于③,将把f(x)的图象向左平移 个单位,得到的函数为
个单位,得到的函数为
y=sin[2(x+ )+
)+ ]=sin(2x
]=sin(2x )=cos2x,所以得到一个偶函数的图象;
)=cos2x,所以得到一个偶函数的图象;
对于④,因为若x∈[0, ],则
],则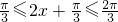 ,所以f(x)在[0,
,所以f(x)在[0, ]上不单调,故④错;
]上不单调,故④错;
故正确的结论是②③
故选C.
点评:此题考查了正弦函数的对称性、三角函数平移的规律、整体角处理的方法,正弦函数的图象与性质是解本题的关键.
分析:将x=
 代入函数f(x)中得到f(
代入函数f(x)中得到f( )=sinπ=0,得到(
)=sinπ=0,得到( )是其对称中心,判断出①错;②对;根据函数图象平移的规律及偶函数的定义判断出③对;根据整体角处理的方法判断出④错.
)是其对称中心,判断出①错;②对;根据函数图象平移的规律及偶函数的定义判断出③对;根据整体角处理的方法判断出④错.解答:对于①②,因为f(
 )=sinπ=0,所以(
)=sinπ=0,所以( )是其对称中心,故①错;②对;
)是其对称中心,故①错;②对;对于③,将把f(x)的图象向左平移
 个单位,得到的函数为
个单位,得到的函数为y=sin[2(x+
 )+
)+ ]=sin(2x
]=sin(2x )=cos2x,所以得到一个偶函数的图象;
)=cos2x,所以得到一个偶函数的图象;对于④,因为若x∈[0,
 ],则
],则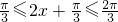 ,所以f(x)在[0,
,所以f(x)在[0, ]上不单调,故④错;
]上不单调,故④错;故正确的结论是②③
故选C.
点评:此题考查了正弦函数的对称性、三角函数平移的规律、整体角处理的方法,正弦函数的图象与性质是解本题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目