题目内容
设函数f(x)=sin(2x+φ)(-π<φ<0),y=f(x)的图象过点(| π | 8 |
(1)求φ;
(2)求函数y=f(x)的周期和单调增区间;
(3)在给定的坐标系上画出函数y=f(x)在区间,[0,π]上的图象.
分析:(1)根据题意可得φ=2kπ+
,结合φ的范围可得k=-1,φ=-
.
(2)利用求周期的公式可得周期;利用整体思想结合正弦函数的性质可得2kπ-
≤2x-
≤2kπ+
,k∈Z,进而得到函数的增区间.
(3)求出x与y的取值结合五点作图法,即可画出函数的图象.
| 5π |
| 4 |
| 3π |
| 4 |
(2)利用求周期的公式可得周期;利用整体思想结合正弦函数的性质可得2kπ-
| π |
| 2 |
| 3π |
| 4 |
| π |
| 2 |
(3)求出x与y的取值结合五点作图法,即可画出函数的图象.
解答:解:(1)∵f(x)的图象过点(
,-1).
∴sin(2×
+φ)=-1,
∴
+φ=2kπ+
,(k∈Z),
所以φ=2kπ+
,
因为-π<φ<0,所以k=-1,φ=-
.
(2)T=
=π,
由(1)知φ=-
,所以f(x)=sin(2x-
),
由题意得 2kπ-
≤2x-
≤2kπ+
,k∈Z,
解得:kπ+
≤x≤kπ+
,k∈Z,
所以函数f(x)=sin(2x-
)的单调增区间为[kπ+
,kπ+
],k∈Z.
(3)
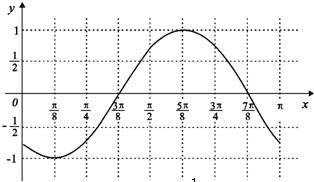
故函数y=f(x)在区间[0,π]上的图象是:
| π |
| 8 |
∴sin(2×
| π |
| 8 |
∴
| π |
| 4 |
| 3π |
| 2 |
所以φ=2kπ+
| 5π |
| 4 |
因为-π<φ<0,所以k=-1,φ=-
| 3π |
| 4 |
(2)T=
| 2π |
| 2 |
由(1)知φ=-
| 3π |
| 4 |
| 3π |
| 4 |
由题意得 2kπ-
| π |
| 2 |
| 3π |
| 4 |
| π |
| 2 |
解得:kπ+
| π |
| 8 |
| 5π |
| 8 |
所以函数f(x)=sin(2x-
| 3π |
| 4 |
| π |
| 8 |
| 5π |
| 8 |
(3)
| x | 0 |
|
|
|
|
π | ||||||||||
f(x)=sin(2x-
|
-
|
-1 | 0 | 1 | 0 | -
|

点评:考查学生已知三角值结合范围求角,以及周期求法和周期函数的单调区间求法与熟练利用五点作图法作三角函数图象.

练习册系列答案
相关题目